Neurons for Dummies - 2

Rieccoci qui per la seconda parte dell'articolo dedicato al neurone.
Se sei capitato qui per sbaglio... SCAPPA!
No scherzo, ovviamente sei invitato a leggere la prima parte qui.
Detto questo, nella prima parte vi ho lasciato con più domande che risposte. Oggi, finalmente, proviamo a fare un po’ di chiarezza.

Capire Dove Si Sbaglia

Iniziamo questo paragrafo ricordando una cosa fondamentale: al centro di tutto ci sono i pesi. Perchè!?
Perché sono l’unico punto su cui possiamo intervenire. Non possiamo certo modificare l'input. Quello arriva dal problema e ce lo becchiamo cosi com'è. Quindi se vogliamo cambiare il valore della funzione di trasferimento, e quindi anche l'output, dobbiamo per forza agire su di loro. Tenendo presente questa premessa e tenendo presente le predizioni fatte nella prima parte, l'obiettivo da raggiungere è passare da questi risultati:

a questi:

In altre parole, vogliamo che tutte le predizioni siano corrette oppure, detto in termini più tecnici, che l'errore nelle predizioni sia il più piccolo possibile. Quindi il primo passo da fare è evidente: misurare l'errore.
Per fare questo è necessario definire una Funzione di Errore o Funzione di Loss, cioè un qualcosa che ci dice quanto siamo lontani dalla situazione ideale, che per semplicità, considereremo come quella in cui l’errore è pari a zero.

Ci sono tantissime funzioni di errore, ognuna pensata per un tipo specifico di problema. Nel nostro caso, che vi ricordo essere il problema AND, siamo in presenza di un problema di classificazione binaria e quindi la funzione più adatta non può che essere la Binary Cross Entropy - BCE.

Andiamo quindi a scrivere la formula:

Dove:

• \(ln(\cdot)\) Logaritmo Naturale
• \(y_i\) Risultato del problema (o True Label) relativo all'i-esimo input.
• \(p_i\) Probabilità predetta dal percettrone per quello stesso input.

Applichiamo questa formula alla seguente tabella di verità:

Per la prima riga abbiamo:

\(y_0 = 0, p_0 = 1 \Rightarrow BCE_0 = -[0 \cdot ln(1) + (1 - 0) \cdot ln(1 - 1)] = -\infty\)

Come si può vedere, l’errore è massimo e in effetti, la predizione è l’opposto esatto del risultato reale.

Applicandola sull'ultima invece si ha:

\(y_3 = 1, p_3 = 1 \Rightarrow BCE_3 = -[1 \cdot ln(1) + (1 - 1) \cdot ln(1 - 1)] = 0\)

In questo caso l'errore è nullo dato che la predizione è esattamente quella attesa.

Sommando tutte le componenti dell'errore, otteniamo l'errore totale:

\(BCE = \sum_{i}{BCE_i}\)

Ma attenzione: in questo caso l’errore risulta infinito e questo può avere senso... ma anche no. Ma tranquilli, tra poco sistemiamo anche questo dettaglio. Per ora, continuiamo così.

Ora che abbiamo introdotto il concetto di errore, sarà più chiaro perché i pesi sono davvero al centro di tutto. Vi ricordate quando vi ho detto che sono l’unico punto su cui possiamo intervenire? Bene...
Ora la vera domanda è: come si modificano i pesi per far sì che l'errore sia il più piccolo possibile?
Imparare, nel contesto delle reti neurali, vuol dire esattamente rispondere a questa domanda. E non solo vogliamo modificare i pesi, ma vogliamo che venga fatto in autonomia. Altrimenti, che intelligenza artificiale sarebbe!? Ma torniamo a noi...
Matematicamente, quale è lo strumento che ci permette di minimizzare o massimizzare una funzione in più variabili?
Ok lo ammetto: è una domanda po' tosta se non avete dimestichezza di analisi matematica. Quindi ve la risparmio e vi do subito la risposta, senza farvi sudare troppo. Parliamo del Gradiente o, per i più facinorosi, il vettore delle Derivate Parziali. Indicando con \(L\) la funzione di errore e con \(w_i\) un peso generico, possiamo scrivere:

Sì, lo so. Sembra ostrogoto. E forse, in questo momento, mi volete anche un po’ picchiare. Ma in realtà, quello che dice ogni componente della formula, in soldoni, è molto semplice:
Quanto incide un generico \(w_i\) sul valore dell'errore, se lo variassi?
E guardando all’intero gradiente, la domanda diventa:
Quale è il valore delle singole \(w_i\) per ottenere il minimo (o massimo) dell’errore?

Se pensate che la complessità finisca qui... mi spiace deludervi, ci sono ancora un paio di step da affrontare.

Errare Errare Errare... Preferisco Ottimizzare

Giusto perché ci piace complicarci la vita, riprendiamo tutta la catena di calcoli che un percettrone esegue, dall’input fino alla misura dell’errore:

• Calcoliamo la somma pesata degli ingressi tramite funzione di trasferimento: \(net=H(x_i, w_i)\)
• Calcoliamo la predizione applicando una funzione di attivazione \(\sigma\) all'output della funzione di trasferimento: \(p=\sigma(net)=\sigma(H(x_i, w_i))\)
• Calcoliamo l'errore tramite una funzione di errore \(L\) sull'output della funzione di attivazione: \(loss =L(p) = L(\sigma(net))=L(\sigma(H(x_i, w_i)))\)

Quindi tutta la catena è rappresentata da questa formula: \(L(\sigma(H(x_i, w_i)))\) Dal paragrafo precedente inoltre, sapete che:

1. Vogliamo minimizzare \(L\).
2. Lo facciamo derivando rispetto i pesi.

Che matematicamente vuol dire scrivere questo:

Per derivare questo mostro, dobbiamo alla regola della catena. Lungi da me scrivere un trattato di analisi matematica, se vuoi trovi una spiegazione rapida qui. Applicando la regola alla nostra funzione composta di errore, otteniamo:

Dove:

• \(\frac{\partial L }{\partial p}\): E' la derivata dell'errore rispetto alla predizione.
• \(\frac{\partial p }{\partial net}\): E' la derivata della funzione di attivazione rispetto l'output della funzione di trasferimento.
• \(\frac{\partial net }{\partial w_i}\): E' la derivata della funzione di trasferimento rispetto un generico peso \(w_i\).

Ragazzi, ci siamo quasi, siamo in dirittura di arrivo. Un ultimo sforzo concettuale...

Sappiamo come calcolare l’errore.
Sappiamo come esprimerlo in funzione dei pesi.
Ora non ci resta che minimizzare.
A scuola, al liceo, all’università, vi insegnano che per trovare un minimo (o un massimo) si usa la derivata prima, ed è ovviamente vero analiticamente parlando. Non sono nessuno per riscrivere le regole della matematica. Ma lasciate che vi faccia una domanda... Come facciamo a minimizzare, analiticamente, una funzione con milioni di parametri? Perché sì, è proprio questo che succede: vogliamo minimizzare l’errore, ma quell’errore è una funzione che dipende da milioni di pesi. Io sono buono e vi faccio vedere l’esempio con un solo percettrone... ma nella realtà, ci sono centinaia e centinaia di percettroni, disposti su più layer, ognuno con molti ingressi.

Non solo non sapremmo calcolarla, ma ci metteremmo una vita e non è nemmeno detto che esista un minimo globale. Quindi vi chiedo: ne vale la pena!?
Ed è qui che intervengono i metodi numerici.
Non saranno eleganti come i metodi analitici, ma diamine se funzionano.
Arriviamo così all'ultimo ingrediente di questo piatto luculliano. La Discesa del Gradiente. Che nel contesto del machine learning è uno (dei tanti) Ottimizzatori. L'idea alla base è semplice e lasciate che ve la spieghi con l’esempio più usato in questi casi: quello dello scalatore bendato. Supponete di trovarvi su una montagna, bendati, e con l’obiettivo di scendere a valle.
Come procedete?
Se sentite che in una direzione il terreno sale, andate nella direzione opposta. E lo fate con passi molto piccoli, perché non sapendo com’è fatto il terreno mica vi mettete a correre giù alla cieca... vero? (Se poi volete farlo non sarò di certo io a fermarvi.) Quello che state facendo è sostanzialmente un controllo locale, per piccoli passi, e non uno globale. Perchè per fare quello globale dovreste conoscere perfettamente la montagna e voi siete bendati. Ecco: la discesa del gradiente è esattamente questo. Procedere per piccoli step la volta perchè non abbiamo conoscenza globale della funzione di errore ma sappiamo localmente, con i pesi a disposizione, come stiamo andando. In formule si scrive così:

Dove:

• \(w_i^{new}\): E' il nuovo peso trovato facendo una piccola variazione di quello corrente. La nuova posizione dello scalatore.
• \(w_i\): E' il peso corrente. La posizione attuale dello scalatore.
• \(\eta\): Si chiama learning rate e indica di quanto variare il peso. Rappresenta l'ampiezza del passo dello scalatore. Se \(\eta = 0\) lo scalatore rimane immobile ed il nuovo peso è uguale al vecchio. Se \(\eta\) è troppo grande è pericoloso perchè non sai dove metti i piedi che matematicamente vuol dire superare la zona dove l'errore era basso.
• \(-\frac{\partial L }{\partial w_i}\): E' la derivata dell'errore rispetto al peso, cioè la direzione in cui l’errore cresce o diminuisce. Il segno meno indica che vogliamo andare nella direzione che fa diminuire l’errore. Rappresenta la capacità dello scalatore di intuire dove si scende e dove si sale.

Graficamente possiamo rappresentarlo così, una entità che cerca sempre di puntare alle zone più basse del grafico.

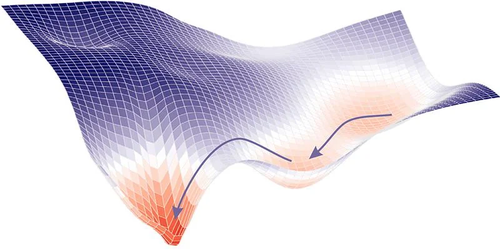Figura 1. Discesa Del Gradiente

Se volete una infarinatura molto a grandi linee di come si arriva alla formula della discesa del gradiente, fate un salto su questo paragrafo, altrimenti passate al successivo e vediamo (finalmente, aggiungerei) un esempio con i numeri.

Ritorno Al Fut... Ehm Al Problema AND

Ed eccoci qui signori, finalmente, a vedere come impara una rete neurale. Vi ricordate del problema AND? Se sì prosegui pure, altrimenti rinfrescati la memoria qui. Vi avevo o no anticipato di non affezionarvi al gradino di Heaviside? E' arrivato il momento di abbandonarlo. Sapete come si dice, morta un'attivazione se ne fa un'altra, e noi prendiamo la funzione Sigmoide. Siete curiosi di sapere il perchè Heaviside non è adatto? Fate un salto qui.

La funzione Sigmoidea ha questa formulazione:

Ed ha questo andamento grafico:

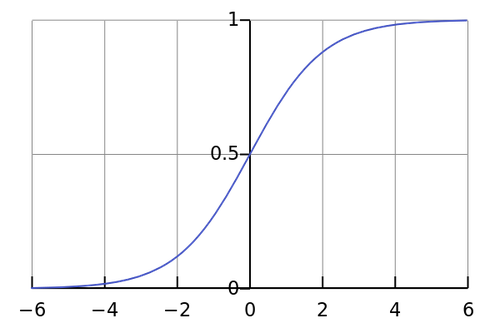Figura 2. Funzione Sigmoide Come potete vedere, l'output è sempre compreso nel range \((0, 1)\).
Voi date \(x=\infty\)? La sigmoide se ne frega e vi da \(1.\)
Voi date \(x=-\infty\)? La sigmoide se ne frega e vi da \(0\).
La sigmoide è troppo forte. Non sfidate la sigmoide perchè tanto perdete.

Prove di forza a parte, ne converrete che la sigmoide è la funzione ideale per rappresentare una probabilità. Una probabilità, in fondo, non è altro che un numero decimale compreso tra \([0, 1]\) dove:

• \(1\) indica sicuramente sì
• \(0\) indica sicuramente no
• \(0.5\) indica boh

Ora che siamo ormai esperti di sigmoidi, riprendiamo in mano il nostro caro percettrone:

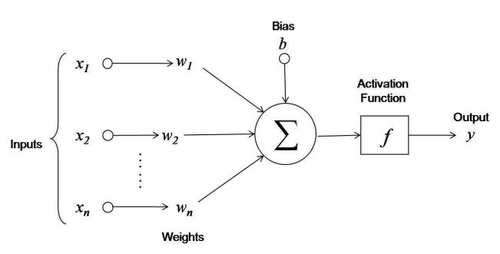Figura 3. Neurone Artificiale

e, riprendiamo i nostri pesi e bias:

• \(w_1 = 0.5\)
• \(w_2 = 0.5\)
• \(b=1\)

Consideriamo il caso \(x_1 = 0, x_2 = 1 \Rightarrow y=0\) L'output della funzione di attivazione sarà: \(net = 0 \cdot 0.5 + 1 \cdot 0.5 + 1 = 1.5\) e di conseguenza l'output della sigmoide è: \( p = \sigma(1.5) \approx 0.817\) Vogliamo calcolare la derivata dell'errore rispetto i pesi (e del bias) giusto?! Ossia:

Ora sappiamo come si calcola un errore, giusto? Abbiamo introdotto la Binary Cross Entropy (BCE) proprio per questo. Quindi, vediamo passo dopo passo cosa succede davvero.

• \(\frac{\partial L }{\partial p}\): E' la derivata della funzione di errore rispetto la predizione. Dall’analisi matematica sappiamo che per la Binary Cross Entropy, si calcola così:
  $$\left( \frac{y}{p} + \frac{ 1 - y}{ 1 - p} \right)$$
  Sostituendo con \(p=0.817\) e \(y=0\), otteniamo:
  $$\left( \frac{0}{0.817} + \frac{ 1 - 0}{ 1 - 0.817} \right) \approx 5.481$$
• \(\frac{\partial p }{\partial net}\): E' la derivata della funzione di attivazione rispetto l'output della funzione di trasferimento. Nel caso della sigmoide, l’analisi matematica ci dice che:
  $$\frac{\partial p }{\partial net} = \sigma(net) \cdot (1 - \sigma(net)) = p \cdot (1 - p)$$
  Sostituendo con \(p=0.817\), otteniamo:
  $$\frac{\partial p }{\partial net} = p \cdot (1 - p) = 0.817 \cdot (1-0.817) \approx 0.149$$
• \(\frac{\partial net }{\partial w_i}\): E' la derivata della funzione di trasferimento rispetto un generico peso. Dall'analisi matematica sappiamo che la sua derivata è:
  $$ \frac{\partial net }{\partial w_i} = \frac{\partial (x_1 \cdot w_1 + x_2 \cdot w_2 + \dots + x_n \cdot w_n + b) }{\partial w_i} = x_i$$
  Insomma, è molto semplice: la derivata è il valore dell’ingresso associato a quel peso. Nel nostro caso:
  $$\frac{\partial net }{\partial w_1} = x_1 = 0$$
  $$\frac{\partial net }{\partial w_2} = x_2 = 1$$
• \(\frac{\partial net }{\partial b}\): E' la derivata della funzione di trasferimento rispetto il bias. Dall'analisi matematica sappiamo che la sua derivata è:
  $$ \frac{\partial net }{\partial b} = \frac{\partial (x_1 \cdot w_1 + x_2 \cdot w_2 + \dots + x_n \cdot w_n + b) }{\partial b} = 1$$
  Come puoi vedere, il bias è sempre derivabile con valore 1, perché è una costante additiva indipendente dagli ingressi.

Ora abbiamo tutto quello che ci serve per calcolare la derivata dell’errore rispetto ai pesi.

Ed infine, ponendo \(\eta = 0.5\), possiamo calcolare i nuovi pesi aggiornati:

Questi nuovi pesi sostituiscono i vecchi, e a quel punto ci ritroviamo con una rete neurale aggiornata. Questo processo si ripete per \(n\) iterazioni (o epoche). E in ogni epoca, addestriamo il percettrone con lo stesso procedimento su tutti i casi del problema.
Ora, senza rifare i calcoli per ogni singolo campione, vediamo cosa succede con lo stesso esempio ma alla seconda epoca. Fate un piccolo atto di fede quando vi dico che i pesi valgono: \(w_1 = 0.356\) \(w_2 = 0.3216\) \(b = 0.1703\) e quindi la funzione di trasferimento vale: \(net = 0 \cdot 0.356 + 1 \cdot 0.3216 + 0.1703 \approx 0.49\) da cui: \( p = \sigma(0.49) \approx 0.66\) Avete visto cos’è successo?
Siamo passati da \(p=0.81\) a \(p=0.66\).
Questo vuol dire che il percettrone ha capito che \(p=0.81\) non era la risposta giusta, e ha iniziato ad abbassare la probabilità che l'output sia \(1\). Con il proseguire dell’addestramento, quel valore continuerà a scendere fino ad arrivare sotto la soglia \(p < 0.5\) cioè: è più probabile che la risposta sia \(0\), che guarda caso è la predizione corretta per quella casistica nel problema AND.
Quello che avete appena visto si chiama Propagazione dell'Errore o, per gli amici, Backpropagation. Ora che siete arrivati fin qui, immaginate questi passaggi, semplici o complessi giudicatelo voi, non su un singolo percettrone ma su centinaia disposti su più layer. Da spararsi vero!?
Ma almeno ci spariamo sapendo come funziona un algoritmo che aggiorna automaticamente i pesi, si adatta al problema da risolvere, e impara dai propri errori.

Conclusioni

Se siete arrivati qui, i miei complimenti.
Non solo avete capito (almeno spero!) un argomento che non è certo una passeggiata di salute (anche se l’abbiamo affrontato con migliaia di semplificazioni e approssimazioni) ma ora sapete perchè dietro le reti neurali non c'è magia... solo molta matematica. Ovviamente non è tutto qui, c'è un mondo intero da scoprire. Ma per il momento accontentiamoci e portiamo a casa questo risultato.

Voglio concludere questo articolo lasciandovi con:

• una tabella di verità arricchita con l’evoluzione dei pesi a ogni epoca
• uno snippet di codice che mette insieme tutto quanto

Considerando come pesi di partenza:

come funzione di attivazione una Sigmoide, e un learning rate pari a:

definiamo la predizione binaria nel seguente modo:

ed indichiamo infine con:

• \(p_{old}/p\) la probabilità predetta prima e dopo dell'aggiornamento dei pesi
• \(\overline{p_{old}}/\overline{p}\) la predizione binaria prima e dopo dell'aggiornamento dei pesi
• \(w_i^{old}/w_i\) i pesi prima e dopo dell'aggiornamento
• \(b^{old}/b\) il bias prima e dopo dell'aggiornamento

I risultati ottenuti su 3 epoche sono i seguenti:

Epoca 1

Epoca 2

Epoca 3

from Perceptron import Perceptron

class WeightedSum(TransferFunction):

    def __call__(self, inputs: np.ndarray, weights: np.ndarray, bias: float) -> float:
        return np.dot(inputs, weights) + bias

    def derive(self, x: float, w: float, b: float) -> (float, float):
        return x, 1.

class Sigmoid(Activation):

    def __call__(self, x: float) -> float:
        threshold = 700
        # Clip per evitare valori estremi
        x = np.clip(x, -threshold, threshold)
        result = (1 / (1 + np.exp(-x))).item()
        result = float(round(result, 5))
        return result

    def derive(self, x) -> float:
        return self(x=x) * (1 - self(x=x))

class BinaryCrossEntropy(Error):

     def __call__(self, true: float, pred: float) -> float:
        true, pred = self.__check_values(true, pred)
        # Clip per evitare valori estremi
        pred = self.__clip_prediction(pred)
        result = - (true * np.log(pred) + (1 - true) * np.log(1 - pred))
        result = float(round(result, 5))
        return result

    def derive(self, true: float, pred: float) -> float:
        true, pred = self.__check_values(true, pred)
        # Clip per evitare valori estremi
        pred = self.__clip_prediction(pred)
        result = - ( true / pred - ( (1 - true) / (1 - pred) ) )
        result = float(round(result, 5))
        return result

class GradientDescent(Optimizer):

    def __call__(self, perceptron: Perceptron, inputs: list, outputs: list, verbose: bool = False) -> float:
        error = 0
        for case, y in zip(inputs, outputs):
            case = np.array(case)

            net_output = perceptron(inputs=case, call_activation=False)
            prediction = perceptron.activation(x=net_output)

            weights = perceptron.weights
            bias = perceptron.bias

            # Derivata dell'errore rispetto la predizione
            dL_dpred = self._error.derive(true=y, pred=prediction)
            # Derivata della funzione di attivazione rispetto la funzione di trasferimento
            dpred_dz = perceptron.activation.derive(x=net_output)
            dL_dz = dL_dpred * dpred_dz

            dL_dwi = []
            dL_dbi = []
            if type(bias) in (int, float):
                bias = [float(bias) for _ in range(len(weights))]

            for w, x, b in zip(weights, case, bias):

                # Derivata dei pesi e del bias rispetto la funzione di trasferimento
                dz_dw, dz_db = perceptron.transfer_function.derive(x=x, w=w, b=b)

                # Derivata dell'errore rispetto ai pesi
                dL_dw = dL_dz * dz_dw
                dL_dwi.append(dL_dw)

                # Derivata dell'errore rispetto al bias
                dL_db = dL_dz * dz_db
                dL_dbi.append(dL_db)

            bias = bias[0]
            dL_db = dL_dbi[0]

            # Calcolo del nuovo bias
            new_bias = float(bias - self._lr * dL_db)

            new_weights = []
            for w, dL_dw in zip(weights, dL_dwi):
                # Calcolo dei nuovi pesi
                new_w = float(w - self._lr * dL_dw)
                new_weights.append(new_w)

            # Aggiornamento del percettrone
            perceptron.weights = np.array(new_weights)
            perceptron.bias = new_bias
            error += self._error(true=y, pred=perceptron(inputs=case))
        return error

optimizer = GradientDescent(lr=0.5, error_function=BinaryCrossEntropy())

perceptron = Perceptron(dimension=2, activation=Sigmoid())
perceptron.weights = np.array([0.5, 0.5])
perceptron.bias = 1.

cases = [[0, 1], [1, 0], [0, 0], [1, 1]]
true = [0, 0, 0, 1]

epochs = 3
for epoch in range(epochs):
    error = optimizer(perceptron=perceptron, inputs=cases, outputs=true, verbose=True)

Siete curiosi di vedere il codice completo? Potete trovarlo qui.
Ultimissima nota prima di chiudere. Questo codice è da considerarsi meramente educativo. Nella realtà si utilizzano librerie come PyTorch o Keras, per astrarre questo livello di complessità. Sappiate in ogni caso che non è finita qui, c'è la parte tre ad attendervi...

Alla Prossima.