Per questo mio primo articolo vorrei parlare di un argomento che mi sta molto a cuore: la Metaeuristica, che non è il nome di un demone assiro ma una famiglia di algoritmi per la risoluzione di problemi computazionali e di ottimizzazione ossia di massimo o di minimo.
Quando ci troviamo davanti a un problema molto grande o complesso, come i problemi NP-Completi, trovare la soluzione
perfetta richiederebbe tempi biblici.
Ed è qui che entrano in gioco loro: le metaeuristiche. Questi algoritmi non promettono l’ottimo assoluto, ma fanno del loro meglio per trovare
soluzioni molto buone, in tempi ragionevoli e con approcci spesso ispirati alla natura ed ai suoi processi.
Basti pensare ad ACO che si basa sul comportamento delle formiche, o PSO ispirato al movimento degli sciami.
Tra i tanti algoritmi metaeuristici, ce n'è uno che mi ha colpito particolarmente, sia per la sua eleganza che per l’originalità dell’ispirazione: il Crystal Structure Algorithm o CryStAl.
Questo algoritmo è ispirato ai processi di formazione di strutture cristalline dove gli elementi: atomi, molecole o ioni, si dispongono in modo ordinato e simmetrico, come avviene
ad esempio nei cristalli di quarzo.
CryStAl si distingue per una caratteristica piuttosto interessante: è un algoritmo senza parametri.
A differenza di molti altri approcci, non richiede di settare valori a mano per controllare il comportamento dell’ottimizzazione,
e gestisce da solo il bilanciamento tra esplorazione (cercare nuove soluzioni in aree diverse) e sfruttamento (raffinare le soluzioni già promettenti),
adattandosi dinamicamente durante il processo.
Il cuore dell’algoritmo si basa su quattro fasi distinte di aggiornamento delle soluzioni,
che permettono di combinare ricerca locale (cioè il miglioramento delle soluzioni vicine a quelle già trovate) e globale
(l’esplorazione di nuove aree nello spazio delle possibili soluzioni) in modo efficace.
Da Dove Nasce L’idea
I minerali solidi i cui componenti costitutivi sono disposti in modo regolare e ripetuto nelle tre direzioni spaziali, sono chiamati cristalli.
Alla base di questa struttura ordinata c’è il reticolo o lattice: una specie di griglia tridimensionale fatta di punti, che si ripete nello spazio.
Di per sé, però, il reticolo non ci dice dove si trovano esattamente gli atomi. Per quello serve un altro pezzo del puzzle: la base,
cioè l’insieme di atomi che si ripete su ogni punto del reticolo. In altre parole: il lattice dice dove mettere qualcosa,
la base dice cosa ci va e come è orientato nello spazio. Eccone un esempio usando puntini blu e orsetti gommosi.
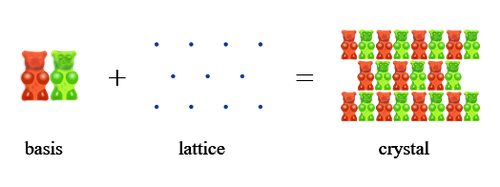 Figura 1. Base + Lattice
Figura 1. Base + Lattice
Grazie ai concetti di reticolo e base, è possibile generare un’infinità di strutture cristalline diverse. Il reticolo, con la sua disposizione regolare di punti, definisce la forma generale del cristallo, mentre la base, cioè l’insieme di atomi che si ripete, ne determina la configurazione interna. Combinando questi due elementi in modi differenti, possiamo ottenere cristalli con geometrie molto varie, alcune regolari e ben note, altre più complesse. Qui sotto trovi alcuni esempi di come queste strutture possono variare:
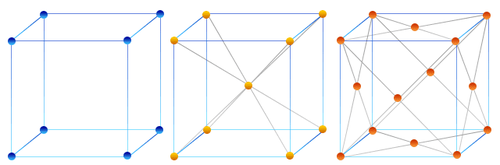 Figura 2. Esempi di Cristalli Cubici
Figura 2. Esempi di Cristalli Cubici
Il lattice, con la sua base, è la struttura ordinata ed ideale che i nostri cristalli artificiali, come vedremo a breve, dovranno cercare di replicare durante l’ottimizzazione.
Il Modello Matematico
Il modello matematico utilizzato dagli autori di questo algoritmo è il modello di Bravais che
permette di descrivere tutti i possibili reticoli che possono esistere nello spazio tridimensionale.
Ogni punto del reticolo si può raggiungere partendo dall’origine e facendo un certo numero intero di passi lungo ciascuna delle tre direzioni:
destra|sinistra, avanti|indietro, sopra|sotto.
Si definisce quindi un vettore posizione tramite la seguente formula:
Dove:
- \(d\) è il numero di dimensioni del cristallo, che è solitamente 3 (a meno che non vivi in un mondo di 4 dimensioni spaziali, in quel caso invitami a casa tua per favore).
- \(n_i\) è un numero intero che indica quanti passi facciamo lungo la direzione \(a_i\).
- \(a_i\) indica la "direzione movimento".
Ora che abbiamo definito \(\overrightarrow{r}\) mettiamolo da parte, ma non preoccupatevi tornerà presto.
Thor mi fulmini se dovessi mai farvi rinunciare alle vostre \(\overrightarrow{r}\).
Torniamo a noi e diamo un’occhiata alle soluzioni candidate.
Ebbene sì: negli algoritmi metaeuristici non c’è una sola soluzione, ma un insieme di soluzioni candidate,
da cui andremo a prendere la migliore.... Ehm dicevo, ogni soluzione candidata (o "cristallo") viene rappresentata come un vettore numerico a
\(d\) dimensioni, cioè una lista di valori:
Dove:
- \(C_i\) è l'\(i\)-esimo cristallo.
- Ogni \(x_{i}^{j}\) indica il valore che assume la variabile \(j\)-esima nei cristallo \(i\).
Per cui la popolazione di cristalli è definita come:
In altre parole, abbiamo una popolazione di \(n\) cristalli, ognuno con \(d\) variabili. Questa matrice, dove ogni riga è un cristallo e ogni colonna una variabile, rappresenta l'intero spazio di ricerca da cui l’algoritmo cercherà di tirare fuori il miglior candidato.
Ok fin qui chiaro (spero)! Ma ora la domanda è... Come diamine si creano questi cristalli?
Presto detto.
Data una funzione di fitness \(f\) che rappresenta il problema da risolvere, i singoli cristalli vengono creati usando
una semplice formula: ogni valore del cristallo viene generato in modo casuale all’interno di un intervallo.
Con:
- \(v_{min}\): Valore minimo che possono assumere le variabili della \(f\).
- \(v_{max}\): Valore massimo che possono assumere le variabili della \(f\).
- \(\xi\): Valore casuale in \(\left[0, 1\right]\)
Detta in parole povere: ogni valore all’interno del cristallo viene scelto casualmente in un intervallo predefinito,
stabilito in base al dominio del problema.
Ognuno di questi cristalli è una soluzione candidata al problema \(f\).
Essere una soluzione candidata, vuol dire che sostituendo gli elementi del cristallo
alle variabili della funzione \(f\), otteniamo un risultato numerico. E ciò che vogliamo è trovare il massimo o il minimo di \(f\), a seconda del problema.
In cristallografia, le basi presenti negli angoli del lattice, ad esempio come le basi presenti ai vertici del cubo in Figura 1, hanno un ruolo fondamentale:
sono l’origine della struttura cristallina. Per analogia, i primi cristalli creati (quelli casuali) vengono chiamati main crystals e
sono indicati con \(C_{r_{main}}\).
Questi main crystals sono il punto di partenza dell’algoritmo che, come anticipato, si articola in quattro fasi di aggiornamento delle soluzioni.
Ognuna corrisponde a una variante della struttura cubica:
- Cubico semplice:
- Cubico con il cristallo migliore:
- Cubico con il cristallo medio:
- Cubico con il cristallo medio e quello migliore:
Come detto all’inizio, questo algoritmo non usa parametri esterni per bilanciare l’esplorazione (trovare nuove soluzioni) e lo sfruttamento (raffinare quelle buone).
Il bilanciamento avviene in modo naturale, proprio grazie alle equazioni di aggiornamento che abbiamo appena visto.
Ma torniamo a noi... abbiamo creato quattro nuovi cristalli partendo dai precedenti. E cosa farne? Lo vedremo tra poco. Prima, lasciate che vi spieghi le stregonerie dietro quei nomi misteriosi:
- \(C_{r_{main}}\): E' un cristallo vecchio selezionato casualmente.
- \(C_{r_{new}}\): E' il nuovo cristallo creato a partire dai precedenti.
- \(C_{r_{old}}\): E' il cristallo originale, prima dell’aggiornamento.
- \(C_{r_{b}}\): E' il cristallo con la configurazione migliore, cioè quello che fornisce il miglior valore per la funzione \(f\).
- \(F_{c}\): E' una media dei valori di un cristallo scelto a caso tra quelli esistenti.
- \(r, r_{1}, r_{2}, r_{3}\): Eccole qui, le nostre vecchie conoscenze! Queste \(r\) non sono più vettori direzionali, ma numeri interi casuali. Così hanno deciso gli autori del paper... e chi sono io per contraddirli?
I cristalli appena creati si utilizzano, come si vedrà nello pseudocodice, per sostituire quelli "vecchi ed imperfetti" con qualcosa di più nuovo e raffinato.
Applicando queste formule per \(n\) volte sugli \(m\) cristalli, l’algoritmo cerca, in modo probabilistico, di trovare quel cristallo che ottimizza al meglio il problema.
Siamo cosi arrivati alla conclusione del modello matematico.
Visione Di Insieme
A questo punto cerchiamo di mettere insieme tutto quanto in pseudocodice:
# Calcolo la prima generazione casuale di cristalli
crystals = create_crystals(min_value, max_value, num_crystal)
# Calcolo il fitness di ogni cristallo
crystal_fitnesses = compute_fitnesses(crystals, problem_to_solve)
# Prendo il cristallo migliore in base al fitness
Cr_b = get_best_crystal(crystals, crystal_fitnesses)
# Inizio Ottimizzazione
for _ in range(0, n_iter):
for current_crystal in crystals:
new_crystals = []
# Calcolo gli r
r, r1, r2, r3 = compute_random_r()
# Prendo un cristallo casuale dalla famiglia
Cr_main = take_random_crystal(crystals)
# Prendo un cristallo casuale dalla famiglia e calcolo la media
Fc = compute_mean(take_random_crystal(crystals))
# Cubico semplice
Cr_new = compute_simple_cubicle(Cr_old, Cr_main, r)
new_crystals.append(Cr_new)
# Cubico con il migliore
Cr_new = compute_cubicle_with_best(Cr_old, Cr_main, Cr_b, r1, r2)
new_crystals.append(Cr_new)
# Cubico con media
Cr_new = compute_cubicle_with_mean(Cr_old, Cr_main, Fc, r1, r2)
new_crystals.append(Cr_new)
# Cubico con migliore e media
Cr_new = compute_cubicle_with_best_and_mean(Cr_old, Cr_main, Cr_b, Fc, r1, r2, r3)
new_crystals.append(Cr_new)
# Clipping per tenere i valori nel range valido
new_crystals = clip_to_min_max(new_crystals, min_value, max_value)
# Calcolo il fitness dei nuovi cristalli
new_crystal_fitnesses = compute_fitnesses(new_crystals, problem_to_solve)
# Seleziono il migliore tra i nuovi
Cr_b_new = get_best_crystal(new_crystals, new_crystal_fitnesses)
# Se il nuovo migliore è meglio dell’attuale, lo sostituisco
if is_new_crystal_fitness_better(Cr_b_new.fitness, current_crystal.fitness):
substitute_current_crystal_with_new_best_one(crystals, current_crystal, Cr_b_new)
# Aggiorno i fitness globali e il cristallo migliore
crystal_fitnesses = compute_fitnesses(crystals, problem_to_solve)
Cr_b = get_best_crystal(crystals, crystal_fitnesses)
Abbiamo quindi definito tutti gli step dell’algoritmo, che permettono, metaforicamente parlando, ai cristalli di modificare la loro struttura interna (cioè i valori numerici) per ottenere la disposizione ottimale della base nel reticolo.
Voglio chiudere con un esempio applicativo di CryStAl su una funzione chiamata Bird Function. che ha questa forma:
dove:
Il grafico della funzione è piuttosto complesso (vedi Figura 3), e trovare il minimo non è affatto banale dal punto di vista analitico.
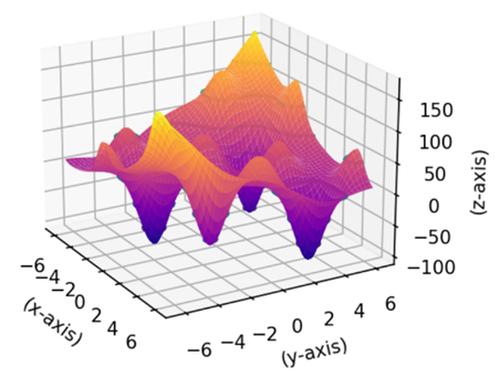 Figura 3. Bird Function
Figura 3. Bird Function
Il suo minimo globale è circa \(f(x, y) = −106.764\) nei punti
- \(p_1 = (4.701, 3.152)\)
- \(p_2 = (−1.582, −3.130)\)
Vediamo cosa succede se proviamo a risolverla con CryStAl:
# Definizione della Bird Function
function = lambda x: np.sin(x[0])*(np.exp(1-np.cos(x[1]))**2) + np.cos(x[1])*(np.exp(1-np.sin(x[0]))**2)+(x[0]-x[1])**2
crystal = CryStAl(function_to_optimize=function, problem_dimension=2, approach="min",
lower_bound=-2 * np.pi, upper_bound=2 * np.pi, num_crystals=10,
num_iterations=20)
best_fitness, Cr_b, _ = crystal.start_crystals_construction(save_history=True, verbose=False, task_name="bird_function")
print(f"Best Crystal Is {Cr_b} with fitness {best_fitness}")
L’output sarà qualcosa tipo:
Best Crystal Is [-1.58090168 -3.14616277] with fitness -106.73618458034184
Non male, vero? Il risultato è molto vicino al minimo teorico, e lo otteniamo con un algoritmo senza parametri, ispirato alla cristallografia, e, ammettiamolo, pure stiloso.
Conclusioni
Spero che questo primo articolo ti abbia incuriosito e magari anche fatto scoprire qualcosa di nuovo! Se vuoi smanettare con l’algoritmo, trovi il codice sorgente completo a questo link. E se ti sei innamorato o innamorata di CryStAl come è successo a me, ti consiglio di dare un’occhiata anche al paper da cui tutto è partito.
Alla prossima.

