BackProp? Anche No

Vi capita mai di svegliarvi al mattino e pensare:
Cavolo, oggi ho proprio voglia di retropropagare l’errore... ma dovrei stare attento alla linea!
No!? Strano, ma contenti voi. In ogni caso, anche se nessuno l'ha chiesto, ho la soluzione che fa per voi: il compromesso giusto tra godimento e gusto. Scherzi a parte, questo articolo è più un esercizio concettuale. Dedicato a chi, come me, pensa che le case siano fatte per starci dentro e azzera la batteria sociale dopo le 20:00. Quest'oggi parlerò di come ho utilizzato l'algoritmo Crystal al posto della backpropagation per modificare, e quindi addestrare, una rete neurale. Non sapete cos'è il Crystal? Male, molto male. Vuol dire che non avete letto il mio articolo a riguardo. Ma tranquilli, potete recuperarlo qui. E se invece vi manca questa fantomatica backpropagation, niente paura: trovate tutta la saga del neurone qui.

Ma Perche!?

Se è questa la vostra domanda, vi ho già detto che l'accoppiata asocialità-20:00 porta a cose strane. Perchè mai dovremmo voler addestrare una rete neurale senza backpropagation che funziona già così bene...?
Vuoi la risposta...?
Perchè posso.
Ironia a parte non è una cosa così infondata. Ripensiamo ai limiti della backpropagation:

• Richiede la derivabilità della funzione di errore e di attivazione.
• Guarda solo localmente la funzione di errore, non globalmente. Questo può portare a minimi locali dove pensate che l'errore sia basso ma solo perchè non potete guardare aldilà del vostro naso.
• Overfitting: Cioè quella situazione in cui avete esagerato con l'addestramento e la rete ha smesso di generalizzare. Conosce benissimo i dati di train, ma non sa gestire quelli nuovi. Per capirci: una cosa è insegnarvi come si fanno le addizioni (generalizzazione), un'altra è insegnarvi solo quanto fa 2+2 (memorizzazione).
• Vanishing/Explosion Gradient: Il gradiente può:
  • Diventare nullo. In questo caso i pesi non variano e la rete smette di imparare.
  • Assumere un valore troppo grande. In questo caso i pesi saranno a loro volta grandi e la rete diventa troppo sensibile agli input. A una piccola variazione dell'ingresso, l'output va in tilt.

Ma basta a parlare male della backpropagation, ditegli le cose in faccia se avete il coraggio. In ogni caso perchè si continua a usarla nonostante tutti questi limiti? Beh perché per ognuno di questi problemi esiste una soluzione per mitigarli. A parte sulla derivabilità, da quella non si scappa. Però puntiamo i piedi e proviamo a guardare una alternativa. Perchè utilizzare la metaeuristica, e in questo caso particolare il Crystal, può superare i limiti sollevati? Vediamoli uno per uno:

• Utilizzando un algoritmo metaeuritisto, non serve calcolare derivate. Quindi potete usare la funzione di errore (e di attivazione) che più vi aggrada. Anche quella pubblicata dall'amico del cugino dello zio su Facebook, quello che sostiene che i poteri forti volevano tenerla nascosta. E si, potete usare anche il gradino di Heaviside.
• Il processo di modifica dei pesi è profondamente diverso da quello della backpropagation. Ricordate lo scalatore che scendeva la montagna a piccoli passi? Bene, qui non vale più. La modifica dei pesi mira a ridurre la funzione di errore globalmente, non localmente. Quindi il rischio di restare bloccati in una "valle" (minimo locale) è sensibilmente ridotto.
• Essendo un processo probabilistico, c’è una bassa probabilità di adattarsi troppo ai dati (overfitting), e questo rende la soluzione più robusta.
• Dato che non si usa più la discesa del gradiente... beh, non c’è più nemmeno il gradiente. Addio problemi di vanishing o exploding gradient.

Ma, come ogni bella storia, anche questa ha i suoi problemi. So che le dimensioni non contano, ma per questi algoritmi contano eccome. Se la rete è troppo grande questa soluzione diventa semplicemente impraticabile e in generale tende a essere meno efficiente della backpropagation. Inoltre potrebbe metterci più tempo per arrivare a convergenza, cioè ad un set di pesi tale per cui la rete può essere considerata buona. Quindi quando scegliere una e quando l'altra?
Come tutto nella vita, dipende. In generale, un approccio metaeuristico può tornare utile in presenza di dati molto rumorosi o quando il rischio di overfitting è particolarmente elevato. In questi casi può valere la pena testare le performance della rete con un metodo alternativo, come Crystal. Detto questo, la backpropagation resta quasi sempre la prima scelta. È molto più efficiente dal punto di vista computazionale, e buona parte delle sue limitazioni può essere attenuata con le tecniche giuste e, cosa ahimè spesso sottovalutata, con una buona pulizia dei dati.

Ma Come!?

I Dati

In questo paragrafo vediamo come, a livello di codice si è proceduto con l'esperimento. Regola numero uno del deep learning, non parlare mai...ah no scusate! I dati. Come dataset ho utilizzato il famosissimo iris, composto da 150 campioni su 4 features che permettono di classificare 3 tipi di iris:

• Iris Setosa
• Iris Virginica
• Iris Versicolor

Se i fiori vi fanno schifo, skippate pure. Altrimenti, sappiate che le features sono:

• Sepal length (cm): Lunghezza del sepalo
• Sepal width (cm): Larghezza del sepalo
• Petal length (cm): Lunghezza del petalo
• Petal width (cm): Larghezza del petalo

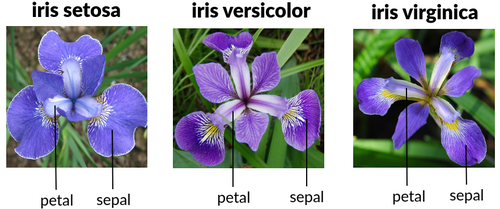Figura 1. Iris Features

A volte può capitare di trovare una quinta colonna: id. Spoiler: non serve a nulla. È solo un identificativo univoco, quindi viene sempre scartato perché non contiene informazione utile. L’obiettivo della rete neurale è semplice sulla carta: indovinare che tipo di Iris abbiamo di fronte, dati i valori numerici delle 4 features.
Questo è un problema entry level nel mondo del deep learning, ma non fatevi fregare: se vi mettessero in mano solo i numeri non ci capireste una fava (per rimanere a tema vegetali).

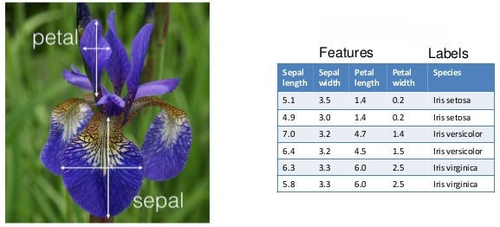Figura 2. Classificazione Iris

La Rete

Volendo comparare le performance di addestramento tra backpropagation e Crystal, ho iniziato molto semplicemente creando due reti neurali identiche, utilizzando il framework PyTorch.
Iniziamo dalla definizione della rete neurale:

class SimpleNet(nn.Module):

    def __init__(self):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(4, 16),
            nn.ReLU(),
            nn.Linear(16, 3)
        )

    def forward(self, x):
        return self.net(x)

L’architettura è molto semplice. E fidatevi, se questa vi sembra complicata... è solo perché non avete ancora visto nulla.
In questa rete abbiamo:

• 4 neuroni di ingresso
• 16 neuroni nel singolo strato nascosto
• 3 neuroni di uscita

Graficamente, potremmo rappresentarla così:

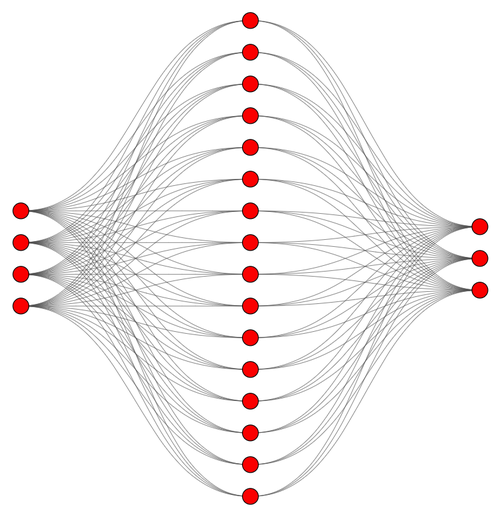Figura 3. Architettura della Rete Neurale

Questi numeri non sono buttati lì a caso. Certo a parte il 16, che potete tranquillamente cambiare in base al vostro umore, all’allineamento dei pianeti o a quanto caffè avete bevuto.

• In ingresso ci devono essere 4 neuroni, perchè 4 sono le features del dataset.
• In uscita ci devono essere 3 neuroni perchè 3 sono i tipi di iris da classificare.

Facendo due calcoli rapidi, abbiamo che i parametri della rete sono:

• Numero di pesi del layer nascosto:

\(4 \cdot 16 = 64\)

• Numero di bias del layer nascosto:

\(16\)

• Numero di pesi del layer di uscita:

\(3 \cdot 16 = 48\)

• Numero di bias del layer di uscita:

\(3\)

Quindi il numero di totale dei parametri è:

\(64 + 48 + 16 + 3 = 131\)

E questo numero è tutt'altro che banale: sarà proprio quello a determinare la dimensione dei cristalli nell’algoritmo Crystal.
Bene ora che abbiamo definito la rete, non dimentichiamoci che ne vogliamo due copie identiche, e per identiche intendo proprio stessa architettura e stessi pesi iniziali, altrimenti che comparazione sarebbe!?
Ora, quando create una rete con PyTorch, i pesi vengono sì inizializzati in modo coerente, ma comunque in maniera casuale. Quindi ho fatto così: ho creato una terza rete fantasma, il cui unico scopo nella vita è fornire i pesi iniziali. Questi vengono poi copiati in entrambe le reti vere che andrò ad allenare. Volendo, potete anche salvare i vostri pesi personalizzati e ricaricarli a piacimento... ma crearli tocca a voi, quindi poi non lamentatevi.
Ecco il codice:

def create_networks(weights: str = "weights.pth"):
    if os.path.exists(weights):
        print(f"Loading weights from {weights}")
        initial_weights = torch.load(weights)
    else:
        print("Creating and Saving new weights...")
        initial_weights = SimpleNet().state_dict()
        torch.save(initial_weights, weights)

    nn_model_backp = SimpleNet()
    nn_model_crystal = SimpleNet()
    nn_model_backp.load_state_dict(deepcopy(initial_weights))
    nn_model_crystal.load_state_dict(deepcopy(initial_weights))
    return nn_model_backp, nn_model_crystal

Se vi state chiedendo perchè ho utilizzato deepcopy vi consiglio caldamento un recappino di OOP e in particolare sul concetto di incapsulamento.
Spoiler: si vuole evitare che modificare una rete cambi anche l'altra, che qua ti distrai un secondo ed è subito anarchia.

Tutto Il Resto

Ora che sappiamo che è definita la nostra rete andiamo a vedere il restante codice. Dato che non ci piace farci mancare nulla, gli ottimizzatori sono stati sviluppati con uno strategy pattern.
La classe astratta e quella contesto sono:

class AOptimizer(ABC):

    def __init__(self, nn_model: nn.Module, loss_function):
        self._model = nn_model
        self._loss_function = loss_function

    @property
    def model(self) -> nn.Module:
        return self._model

    @model.setter
    def model(self, nn_model) -> None:
        self._model = nn_model

    @property
    def loss_function(self) -> loss._WeightedLoss:
        return self._loss_function

    @loss_function.setter
    def loss_function(self, loss_function: loss._WeightedLoss) -> None:
        self._loss_function = loss_function

    @abstractmethod
    def optimize(self, X_train: np.ndarray, y_train: np.ndarray) -> None:
        raise NotImplementedError

    @staticmethod
    @abstractmethod
    def get_name() -> str:
        raise NotImplementedError

    def evaluate(self, X_test: np.ndarray, y_test: np.ndarray) -> float:
        X_test = torch.tensor(X_test, dtype=torch.float32)
        y_test = torch.tensor(y_test, dtype=torch.long)
        preds = self._model(X_test).argmax(dim=1)
        acc = (preds == y_test).float().mean()
        return acc

class Optimizer:

    def __init__(self, strategy: AOptimizer = None):
        self._strategy = strategy

    @property
    def strategy(self) -> AOptimizer:
        return self._strategy

    @strategy.setter
    def strategy(self, strategy: AOptimizer) -> None:
        self._strategy = strategy

    def optimize(self, X_train: np.ndarray, y_train: np.ndarray) -> None:
        self._strategy.optimize(X_train, y_train)

    def evaluate(self, X_test: np.ndarray, y_test: np.ndarray) -> float:
        return self._strategy.evaluate(X_test, y_test)

Mentre le strategie concrete sono due.
Quella che implementa la backpropagation:

class BackpropOptimizer(AOptimizer):

    def __init__(self, nn_model, loss_function):
        super().__init__(nn_model=nn_model, loss_function=loss_function)

    @staticmethod
    def get_name():
        return "Backprop"

    def optimize(self, X_train: np.ndarray, y_train: np.ndarray) -> None:

        print(f"Start optimization for {BackpropOptimizer.get_name()} Strategy")

        X_train_t = torch.tensor(X_train, dtype=torch.float32)
        y_train_t = torch.tensor(y_train, dtype=torch.long)
        train_loader = DataLoader(TensorDataset(X_train_t, y_train_t), shuffle=False)

        opt = optim.Adam(self._model.parameters(), lr=0.01)
        for epoch in range(21):
            for xb, yb in train_loader:
                opt.zero_grad()
                out = self._model(xb)
                loss = self._loss_function(out, yb)
                loss.backward()
                opt.step()

            if epoch % 10 == 0:
                print(f"Epoch {epoch}, Loss: {loss.item():.4f}")

        acc = self.evaluate(X_test=X_train, y_test=y_train)
        print(f"Accuracy on Train Set: {acc:.2%}")

e quella che implementa il Crystal:

class CrystalOptimizer(AOptimizer):

    def __init__(self, nn_model, loss_function):
        super().__init__(nn_model=nn_model, loss_function=loss_function)

    ...

    @staticmethod
    def get_name() -> str:
        return "Crystal"

    def _is_new_fitness_better(self, old_crystal_fitness, new_crystal_fitness) -> bool:
        return new_crystal_fitness < old_crystal_fitness

    def _flat_weights(self) -> np.ndarray:
        weights = []
        for p in self._model.parameters():
            weights.append(p.data.view(-1))
        weights = torch.cat(weights).detach().cpu().numpy()
        return weights

    def _create_crystals(self, lb: int, ub: int, nb_crystal: int) -> (np.array, int, int):
        base_weights = self._flat_weights()
        dim = base_weights.size
        random_crystals = np.random.uniform(low=lb, high=ub, size=(nb_crystal - 1, dim))
        crystals = np.vstack([base_weights, random_crystals])
        print(f"Created {crystals.shape[0]} Crystals With {crystals.shape[1]} Elements")
        return crystals

    def _assign_weights(self, crystal: np.ndarray) -> None:
        cum_p = 0
        for p in self._model.parameters():
            total_params = p.numel()
            tensor = torch.tensor(crystal[cum_p:cum_p + total_params])
            reshaped_tensor = tensor.view(p.shape)
            p.data.copy_(reshaped_tensor)
            cum_p += total_params

    def _evaluate_crystals(self, crystals: np.ndarray, X_train: torch.Tensor, y_train: torch.Tensor) -> (np.ndarray, float, int):
        losses = []
        for crystal in crystals:
            self._assign_weights(crystal)
            with torch.no_grad():
                outputs = self._model(X_train)
                loss = self._loss_function(outputs, y_train)

            losses.append(loss.item())

        fitnesses = np.array(losses).reshape(-1, 1)
        best_index = np.argmin(fitnesses)
        best_value = fitnesses[best_index, 0]
        return fitnesses, best_value, best_index

    def optimize(self, X_train: np.ndarray, y_train: np.ndarray) -> None:
        print(f"Start optimization for {CrystalOptimizer.get_name()} Strategy")

        X_train_t = torch.tensor(X_train, dtype=torch.float32)
        y_train_t = torch.tensor(y_train, dtype=torch.long)

        lower_bound, upper_bound = -2, 2
        nb_crystal = 15
        nb_iterations = 60
        crystals = self._create_crystals(lb=lower_bound, ub=upper_bound, nb_crystal=nb_crystal)
        fitnesses, best_fitness, best_index = self._evaluate_crystals(crystals=crystals, X_train=X_train_t, y_train=y_train_t)
        Cr_b = crystals[best_index]
        for i in range(0, nb_iterations):
            for crystal_idx in range(0, nb_crystal):
                new_crystals = np.array([])
                Cr_main = self._take_random_crystals(crystals=crystals, nb_random_crystals_to_take=1, nb_crystal=nb_crystal).flatten()
                Cr_old = crystals[crystal_idx]
                Fc = self._take_random_crystals(crystals=crystals, nb_crystal=nb_crystal).mean(axis=0)
                r, r_1, r_2, r_3 = self.__compute_r_values()
                Cr_new = self._compute_simple_cubicle(Cr_old=Cr_old, Cr_main=Cr_main, r=r)
                new_crystals = np.hstack((new_crystals, Cr_new))
                Cr_new = self._compute_cubicle_with_best_crystals(Cr_old=Cr_old, Cr_main=Cr_main, Cr_b=Cr_b, r_1=r_1, r_2=r_2)
                new_crystals = np.vstack((new_crystals, Cr_new))
                Cr_new = self._compute_cubicle_with_mean_crystals(Cr_old=Cr_old, Cr_main=Cr_main, Fc=Fc, r_1=r_1, r_2=r_2)
                new_crystals = np.vstack((new_crystals, Cr_new))
                Cr_new = self._compute_cubicle_with_best_and_mean_crystals(Cr_old=Cr_old, Cr_main=Cr_main, Cr_b=Cr_b, Fc=Fc, r_1=r_1, r_2=r_2, r_3=r_3)
                new_crystals = np.vstack((new_crystals, Cr_new))
                new_crystals = np.clip(new_crystals, a_min=lower_bound, a_max=upper_bound)
                new_crystal_fitnesses, new_crystal_best_fitness, new_crystal_best_index = self._evaluate_crystals(crystals=new_crystals, X_train=X_train_t, y_train=y_train_t)
                current_crystal_fitness = fitnesses[crystal_idx][0]
                if self._is_new_fitness_better(old_crystal_fitness=current_crystal_fitness, new_crystal_fitness=new_crystal_best_fitness):
                    crystals[crystal_idx] = new_crystals[new_crystal_best_index]

            fitnesses, best_fitness, best_index = self._evaluate_crystals(crystals=crystals, X_train=X_train_t, y_train=y_train_t)
            Cr_b = crystals[best_index]
            if i % 10 == 0:
                print(f"Iter {i}. Current Best Crystal Fitness Is {best_fitness}")
            self._assign_weights(crystal=Cr_b)
        acc = self.evaluate(X_test=X_train, y_test=y_train)
        print(f"Accuracy on Train Set: {acc:.2%}")

Non mi soffermerò sulla classe relativa alla backpropagation. Vi basti sapere che è stato utilizzato PyTorch che permette di avere un alto livello di astrazione e ci risparmia il manicomio.
Ma Luca, io voglio sapere come funziona!
Se ti sei fatto questa domanda, vuol dire che non hai letto la serie di articoli sul neurone quindi RECUPERALI. Concentriamoci invece sulla classe relativa al Crystal. Anche qui mi limiterò a spiegare solo alcuni pezzi di codice e sai perchè? Perchè l'ho già spiegato in un articolo dedicato quindi sì, anche sta volta è colpa tua. Vai e recupera anche quello.
Ma bando ai rimproveri e iniziamo vedendo come viene creata la popolazione iniziale di cristalli grezzi. Se stampassimo la struttura della rete con questo snippet:

from SimpleNet import SimpleNet

net = SimpleNet()
for name, p in net.named_parameters():
    print(name, "|", p.shape)

otterremmo il seguente output:

net.0.weight | torch.Size([16, 4])
net.0.bias | torch.Size([16])
net.2.weight | torch.Size([3, 16])
net.2.bias | torch.Size([3])

Cosa stiamo guardando esattamente? Una sequenza di matrici e vettori.

• Il primo elemento (net.0.weight) è una matrice di pesi con 16 righe (una per neurone) e 4 colonne (una per feature). Come so che sono pesi? È scritto proprio lì, sulla sinistra.
• Subito dopo c’è un vettore di bias (net.0.bias) con 16 elementi, uno per neurone. Come so che sono bias?! Perchè è sempre lì, sulla sinistra.

Stesso discorso vale per le altre due righe.
C'è un piccolo problema: i cristalli sono semplici liste di float mentre la rete neurale lavora con matrici e vettori. Quindi dobbiamo adattare la nostra sequenza di parametri.
Vediamo questo snippet:

    def _flat_weights(self) -> np.ndarray:
        weights = []
        for p in self._model.parameters():
            weights.append(p.data.view(-1))
        weights = torch.cat(weights).detach().cpu().numpy()
        return weights

    def _create_crystals(self, lb: int, ub: int, nb_crystal: int) -> np.array:
        base_weights = self._flat_weights()
        dim = base_weights.size
        random_crystals = np.random.uniform(low=lb, high=ub, size=(nb_crystal - 1, dim))
        crystals = np.vstack([base_weights, random_crystals])
        print(f"Created {crystals.shape[0]} Crystals With {crystals.shape[1]} Elements")
        return crystals

    def optimize(self, X_train: np.ndarray, y_train: np.ndarray) -> None:
        ...
        nb_crystal = 15
        lower_bound, upper_bound = -2, 2
        crystals = self._create_crystals(lb=lower_bound, ub=upper_bound, nb_crystal=nb_crystal)

Cosa stiamo facendo qui?

• Con _flat_weights iteriamo su tutti i parametri della rete, cioè le matrici e i vettori dei pesi e dei bias. Ognuna di queste strutture viene flattenata, cioè trasformata in una lista. Perdiamo la struttura, ma non il contenuto. Tutti questi vettori vengono concatenati insieme in un’unica grande lista di 131 elementi (nel nostro caso specifico), che rappresenta tutti i pesi e bias della rete.
• Questa lista rappresenta il primo cristallo della rete, e fornisce informazioni alla funzione _create_crystals per creare tutti gli altri in maniera casuale ma della stessa dimensione. Abbiamo in uscita una matrice dove ogni riga, ossia ogni cristallo, è l'intero set di parametri della rete neurale.

• I parametri lower_bound, upper_bound = -2, 2 e nb_crystal = 15, specificano rispettivamente:

  • i valori massimi e minimi che possono assumere i pesi.
  • il numero di cristalli desiderati.

Abbiamo quindi una popolazione di 15 cristalli, ognuno con 131 elementi che spaziano da -2 a 2. Questi valori sono iperparametri. Come sono stati scelti? A sentimento. In generale: meno elementi nella popolazione = algoritmo più veloce. Inoltre non vogliamo una rete con pesi troppo grandi per non renderla troppo sensibile agli input.
Continuiamo vedendo un altro snippet essenziale:

    def _assign_weights(self, crystal: np.ndarray) -> None:
        cum_p = 0
        for p in self._model.parameters():
            total_params = p.numel()
            tensor = torch.tensor(crystal[cum_p:cum_p + total_params])
            reshaped_tensor = tensor.view(p.shape)
            p.data.copy_(reshaped_tensor)
            cum_p += total_params

    def _evaluate_crystals(self, crystals: np.ndarray, X_train: torch.Tensor, y_train: torch.Tensor) -> (np.ndarray, float, int):
        losses = []
        for crystal in crystals:
            self._assign_weights(crystal)
            with torch.no_grad():
                outputs = self._model(X_train)
                loss = self._loss_function(outputs, y_train)

            losses.append(loss.item())

        fitnesses = np.array(losses).reshape(-1, 1)
        best_index = np.argmin(fitnesses)
        best_value = fitnesses[best_index, 0]
        return fitnesses, best_value, best_index

    def optimize(self, X_train: np.ndarray, y_train: np.ndarray) -> None:
        ...
        crystals = self._create_crystals(lb=lower_bound, ub=upper_bound, nb_crystal=nb_crystal)
        fitnesses, best_fitness, best_index = self._evaluate_crystals(crystals=crystals, X_train=X_train_t, y_train=y_train_t)
        Cr_b = crystals[best_index]
        for i in range(0, nb_iterations):
            for crystal_idx in range(0, nb_crystal):
                ...
                new_crystal_fitnesses, new_crystal_best_fitness, new_crystal_best_index = self._evaluate_crystals(crystals=new_crystals, X_train=X_train_t, y_train=y_train_t)
                current_crystal_fitness = fitnesses[crystal_idx][0]
                if self._is_new_fitness_better(old_crystal_fitness=current_crystal_fitness, new_crystal_fitness=new_crystal_best_fitness):
                    crystals[crystal_idx] = new_crystals[new_crystal_best_index]
            fitnesses, best_fitness, best_index = self._evaluate_crystals(crystals=crystals, X_train=X_train_t, y_train=y_train_t)
            Cr_b = crystals[best_index]
            self._assign_weights(crystal=Cr_b)

Entriamo nel cuore pulsante dell’algoritmo, dove i cristalli vengono finalmente messi alla prova. Quello che vedete è l’inizio dell’iterazione evolutiva che consente ai cristalli di evolversi, mutare e, si spera, migliorare. Ma visto che l’evoluzione l’abbiamo già spiegata in un altro articolo, qui ci concentriamo su come usiamo questi benedetti cristalli.

• Per ogni cristallo, la funzione _evaluate_crystals fa tre cose fondamentali:

  • Trasforma il cristallo in parametri di rete compatibili.
  • Assegna quei parametri alla rete neurale.
  • Valuta quanto il cristallo è bravo a classificare i fiori usando una loss function (che vediamo a brevissimo).

• La funzione _assign_weights è responsabile della magia nera. Prende una semplice lista piatta di numeri (il cristallo), e la trasforma di nuovo in matrici e vettori compatibili con la rete neurale. Come ci riesce? Vediamolo passo per passo:

  • Si cicla sulla rete neurale accedendo ai suoi parametri (pesi e bias) con self._model.parameters().
  • Per ogni parametro:
    • Con p.numel() scopriamo quanti elementi servono.
    • Prendiamo esattamente quel numero di elementi dalla lista del cristallo: crystal[cum_p:cum_p + total_params].
    • Li trasformiamo nella forma corretta (matrice o vettore) con: tensor.view(p.shape).
    • Li assegniamo al layer: p.data.copy_(reshaped_tensor)
    • E aggiorniamo il contatore cum_p, così la prossima volta prenderemo i valori giusti dalla posizione giusta.

In pratica, visto che abbiamo costruito i cristalli seguendo esattamente l’ordine dei parametri della rete, adesso possiamo ricostruire la rete neurale a partire dal cristallo, pezzo dopo pezzo. Elegante, no?

Eccoci arrivati al momento della verità: mettere a confronto backpropagation e Crystal su un terreno comune.

nn_model_backp, nn_model_crystal = create_networks()
X_train, X_test, y_train, y_test = get_data()
loss = nn.CrossEntropyLoss()

backprop_opt = BackpropOptimizer(nn_model=nn_model_backp, loss_function=loss)
crystal_opt = CrystalOptimizer(nn_model=nn_model_crystal, loss_function=loss)
opt = Optimizer()

for concrete_strategy in [backprop_opt, crystal_opt]:
    start = time.perf_counter()

    opt.strategy = concrete_strategy

    acc = opt.evaluate(X_test=X_test, y_test=y_test)
    print(f"Accuracy Before Train On Test Set with {concrete_strategy.get_name()}: {acc:.2%}")

    opt.optimize(X_train=X_train, y_train=y_train)
    acc = opt.evaluate(X_test=X_test, y_test=y_test)
    print(f"Accuracy After Train On Test Set with {concrete_strategy.get_name()}: {acc:.2%}")

    end = time.perf_counter()
    elapsed = end - start
    print(f"Elapsed: {elapsed:.4f}s")

Come si può leggere dal codice, dopo aver istanziato le due reti neurali identiche, e aver istanziato train set e test set, definiamo la funzione di loss, in questo caso la buona vecchia Cross Entropy, perfetta per problemi di classificazione. La funzione di loss è richiesta, insieme alle reti neurali, come parametro dai costruttori delle classi concrete degli ottimizzatori. Per ogni ottimizzatore istanziato quello che si fa è:

• Si stampa l'accuratezza sul test set prima del train. Ovviamente l'accuratezza pre train, sarà identica per le due strategie perchè hanno entrambe lo stesso set di pesi e condividono lo stesso test set.
• Si avvia il processo di ottimizzazione richiamando il metodo optimize(X_train=X_train, y_train=y_train) che prende in ingresso il train set.
• Si stampa l'accuratezza sul test set dopo il processo di ottimizzazione, ossia dopo il train.
• Si stampa il tempo di elaborazione.

L'output dovrebbe essere simile al seguente:

Accuracy Before Train On Test Set with Backprop: 36.67%
Start optimization for Backprop Strategy
Epoch 0, Loss: 0.3089
Epoch 10, Loss: 0.0071
Epoch 20, Loss: 0.0010
Accuracy on Train Set: 97.50%
Accuracy After Train On Test Set with Backprop: 96.67%
Elapsed: 4.4316s
Accuracy Before Train On Test Set with Crystal: 36.67%
Start optimization for Crystal Strategy
Created 15 Crystals With 131 Elements
Iter 0. Current Best Crystal Fitness Is 1.5699747800827026
Iter 10. Current Best Crystal Fitness Is 0.38595184683799744
Iter 20. Current Best Crystal Fitness Is 0.16885297000408173
Iter 30. Current Best Crystal Fitness Is 0.14107681810855865
Iter 40. Current Best Crystal Fitness Is 0.09387028217315674
Iter 50. Current Best Crystal Fitness Is 0.09387028217315674
Accuracy on Train Set: 96.67%
Accuracy After Train On Test Set with Crystal: 93.33%
Elapsed: 1.1045s

I risultati non saranno esattamente identici ogni volta dato che i processi sono probabilistici, ma in media le performance si avvicinano sorprendentemente. E ora, rullo di tamburi: il Crystal è risultato più veloce. E no, non ho sbagliato tutto quello che ho detto all’inizio. Semplicemente, in questo caso specifico:

• La rete è piccola
• I parametri sono pochi
• 15 cristalli per 50 iterazioni fanno solo 750 valutazioni
• Niente derivate da calcolare

Quindi sì, è plausibile che batta la backpropagation in velocità. Ma attenzione: al crescere della complessità del problema e delle dimensioni della rete, i cristalli diventano sempre più grandi, e le iterazioni necessarie aumentano. E in quel caso la backpropagation se la gode comandandosela.

Conclusioni

Siamo finalmente giunti alla conclusione di questo articolo. Magari vi sarà utile nella vita o magari no, ma posso dire che è stato un ottimo esercizio concettuale che mi ha permesso di affrontare diversi argomenti interessanti. Come sempre, se siete curiosi di leggere l'intero codice sorgente, potete scaricarlo da qui.

Alla Prossima.