Rieccoci con la seconda parte della serie dedicata alle Neural ODE. Se il primo articolo è stata una violenza mentale questo lo sarà un po' meno. Ma non illudetevi: non è ancora una passeggiata di salute. Abbiamo già affondato le mani nella melma di derivata, integrale ed equazione differenziale. E ora, visto che ci siamo già rovinati la manicure, tanto vale farla finita e rispondiamo a una delle domande lasciate in sospeso nel primo articolo. Quindi senza indugio (con segugio) iniziamo, e vediamo come si risolve una ODE.
ODE Al Metodo
Lo so, lo sento che non vedevate l'ora di sapere come si risolve una ODE e finalmente eccoci qua. Come si risolve una ODE? La risposta rapida è dipende. Come sempre nella vita ci sono delle alternative: una elegante e una brutale.
Da un lato abbiamo i metodi analitici. Sono quelli di classe e ben vestiti, come uno stagista in una Big 4. Sono quei metodi che ci danno una formula esatta della soluzione. Ora sorge una domanda. Se sono così belli e perfetti, perché è necessario avere delle alternative? Perché, proprio come uno stagista in una Big 4, quando il gioco si fa duro questi metodi non bastano e bisogna chiedere aiuto ad altri.
E qui entrano in gioco i metodi numerici. Gli spavaldi della situazione. Ma sì chiamiamoli pure gli apprendisti di una Big 4 (amici delle Big 4, ovviamente si fa per ridere eh, pace e amore.). Se ne fregano di eleganza e di formule esatte, testa bassa e portano a casa il risultato. Procedono a piccoli passi stimando la soluzione punto per punto. Non sono esatti, è vero. Ma a volte, sono l’unica via praticabile.
In sintesi, scegliere il metodo giusto dipende da due cose:
- Da voi: magari non avete voglia di sudare su una soluzione analitica o più semplicemente non vi serve.
- Dal problema: perché alcune ODE, semplicemente, non hanno una soluzione analitica. E quando succede, ciò che volete voi vale quanto il due di bastoni con briscola a spade.
Metodi Analitici
Iniziamo dai bellocci della situazione. I metodi analitici riescono, almeno quando tutto va bene, a tirar fuori la formula chiusa della funzione che risolve l’equazione. Questi metodi sono applicabili solo in condizioni particolari, spesso ideali, che di fatto potete trovare solo sui libri di testo universitari. Non c'è un unico metodo a disposizione, ma in base alla struttura della ODE ne abbiamo a disposizione diversi:
- Metodo di Separazione delle Variabili
- Metodo del Fattore Integrante
- Metodo di Somiglianza
- Metodo della Trasformata di Laplace
- ...e altri ancora, ma fidatevi, la lista è lunga
Li vedremo tutti? Assolutamente no. Vedremo i primi due giusto per mostrare che non sto inventando roba, ma se volete una panoramica completa e dettagliata, vi consiglio di dare una letta qui.
Separazione delle Variabili
Il metodo di separazione delle variabili è uno di quei metodi che vabbè dai è fichissimo, ma quando mai potrò usarlo?. Infatti è utilizzabile solo quando una ODE può essere scritta in questo modo:
Avere questa struttura ci permette di fare questo:
Cioè moltiplicato entrambi i termini dell'equazione per \(dt\) e diviso entrambi per \(f(y)\). In pratica abbiamo separato, portando da un lato tutto ciò che è relativo ad \(y\) e dall'altro tutto ciò che è relativo a \(t\). Per rendere meglio l'idea, provate a giocare con questa ODE:
Imprecate, bestemmiate e sbattete pure la testa al muro, non riuscirete mai a separare \(y\) da \(t\). In almeno uno dei membri dell'equazione ci sarà sempre un intruso, sia esso relativo a \(y\) o a \(t\).
A questo punto, non resta che integrare entrambi i membri dell'uguaglianza risolvendo la ODE
Esempio
Bene finalmente possiamo vedere un esempio. In questo paragrafo vi avevo buttato lì una ODE insieme alla sua soluzione, senza dirvi da dove è scappata fuori. Riprendiamola:
Questa si adatta molto bene alla separazione delle variabili, infatti è già scritta nella forma che ci serve:
dove:
- \(f(y) = y(t)\)
- \(g(t) = 3\)
Quindi facciamo i nostri barbatrucchi per separare le \(y\) dalle \(t\):
Dato che ora siamo dei draghi con le derivate, se vediamo \(d-qualcosa\), sappiamo che è un infinitesimo e che dobbiamo integrare per risalire alla primitiva. Integriamo quindi, in maniera indefinita, entrambi i termini.
Dalla tabella degli integrali notevoli risolviamo molto agevolmente questi integrali:
da cui:
Dato che \(C_2\) e \(C_1\) sono due costanti arbitrarie, che possono assumere qualsiasi valore (riflettete su questo punto, qui) possiamo, a cuor leggero, porre:
Quindi tornando alla soluzione si ha:
Per isolare la \(y\) dobbiamo invertire il logaritmo naturale, quindi usiamo entrambi i termini come esponenti di \(e\) e otteniamo:
Per lo stesso principio di prima, abbiamo che \(e^C\) è una costante arbitraria per cui anche qui possiamo semplicemente cambiargli nome e scriviamo:
da cui
Questo a dimostrazione che non ho detto minchiate nella parte 1. Tutto torna e il mondo può riprendere il suo moto di rotazione. Ora ci rimane solo l'amaro in bocca del "si ma quanto vale sto' K?" Il problema non ci fornisce abbastanza informazioni, quindi per come è posto non possiamo saperlo. Per quantificare \(K\) ci serve un problema di Cauchy. Cosa rimane...? Ah sì, da mostrare l'andamento grafico. Eccolo qui
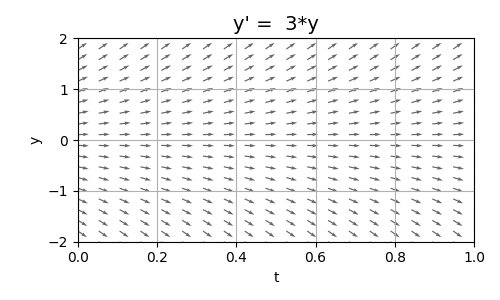 Figura 1. Plot di \(y=K \cdot e^{3t}\)
Figura 1. Plot di \(y=K \cdot e^{3t}\)
Commentiamo questo grafico. Come sapete, o almeno dovreste dalla prima parte, è un grafico di Direzione di Campo. Anche se conosciamo la forma generale della soluzione, senza sapere quanto vale \(K\) non possiamo tracciarne l’andamento preciso. Il campo di direzione però ci aiuta: ci mostra come si comportano le soluzioni per valori diversi di \(K\), anche senza conoscerli esplicitamente. Quello che si nota è che abbiamo tre famiglie di soluzioni:
- La famiglia crescente: le frecce, per \(y>0\), divergono verso l'alto.
- La famiglia decrescente: le frecce, per \(y<0\), divergono verso il basso.
- La famiglia costante: composta da un solo e soletto elemento, sempre nullo, corrispondente a \(y=0\).
Fattore Integrante
Avete presente quella ODEina (che non è la moglie di ODEino... Ok, mi faccio schifo da solo), che nel paragrafo precedente non poteva essere risolta? Intendo questa:
Piccola nota, la \(y\) è sempre in funzione del tempo, quindi capiterà che leggiate \(y\) e non \(y(t)\), ma sono del tutto equivalenti.
Bene, con il metodo del fattore integrante possiamo arrivare dove la separazione delle variabili non è arrivata. Questo metodo richiede che la ODE sia lineare di primo grado (leggi qui), e che possa essere scritta nella forma:
Formula 1. Forma Base Fattore Integrante
a questo punto il metodo richiede la creazione di fattore integrante definito come:
e moltiplichiamo tutti i termini della nostra ODE per \(\mu (t)\):
Formula 2. Fattore Integrante
A questo punto ricorriamo ad un trucchetto matematico. Prendiamo la regola di derivazione del prodotto tra funzioni:
Formula 3. Derivata Del Prodotto
Dato che siamo in presenza di una ODE del primo grado, abbiamo che
da cui
perché stiamo integrando una derivata, e
dato che \(e\) è anche la base del logaritmo naturale. Quindi:
Facendo le dovute sostituzioni nella Formula 3 abbiamo:
Dato che l'ultima volta che ho controllato, valeva ancora la Formula 2, possiamo scrivere:
Integrando entrambi i membri abbiamo:
Infine signore e signori, dividendo per \(\mu(t)\) arriviamo alla formulazione finale della \(y\)
Formula 4. Soluzione Del Fattore Integrante
Come abbiamo visto, con non poche difficoltà ammettiamolo, quando possiamo applicare il fattore integrante abbiamo una "formuletta" confezionata pronta per esplicitare la tanto agognata \(y\). Direi senza indugio, di vedere un esempio.
Esempio
La ODE che volevamo risolvere era questa
Giusto!? Bene, anzi ottimo! Si presta all'utilizzo del fattore integrante. Quindi riprendiamo la ODE ma stavolta risolviamo un problema di Cauchy e supponiamo di avere non solo la ODE, ma anche qual è il valore della soluzione \(y(t)\) in \(t=0\), che poniamo essere \(0\) (ma poteva anche essere \(y(t)=5\) in \(t=214\), ci basta conoscere almeno un valore della funzione in un istante preciso):
Partiamo dalla ODE:
Quindi:
- \(p(t) = -2t\)
- \(q(t) = t\)
Dalla formula della soluzione del fattore integrante, dobbiamo calcolare:
Quindi abbiamo:
Ora dobbiamo risolvere
Lo sento, sento il terrore che attanaglia i cuori di chi ha fatto Analisi 1, perché la risoluzione di questo integrale richiede il metodo della sostituzione, che non sto qui a spiegare ma vi lascio una fonte per approfondire. Posto quindi
Tornando alle variabili originali si ha:
e quindi:
Tornando alla nostra \(y\) abbiamo:
Dove, essendo costanti arbitrarie, abbiamo posto
Quindi
Ricordiamoci che siamo in un problema di Cauchy dove per \(t=0\), \(y=0\) per cui:
Grazie alla condizione iniziale, abbiamo il valore di \(K\), per cui possiamo calcolare il valore di \(y\) in tutti gli istanti temporali. Se siete stati attenti, sapete quanto vale \(y\) in \(t=0\). Facciamo quindi il calcolo per \(t=1\):
Esattamente come ci avevo anticipato, avere una condizione iniziale permette di ottenere il valore della ODE in qualsiasi istante temporale \(t\). Ovviamente la condizione iniziale può cambiare l'andamento della ODE. Diamo una occhiata al diagramma di direzione di campo e di fase
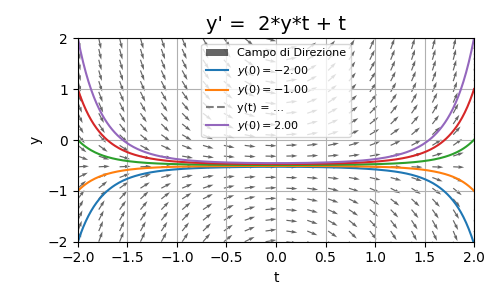 Figura 2. Plot di \(y=-\frac{1}{2} + K \cdot e^{t^2}\)
Figura 2. Plot di \(y=-\frac{1}{2} + K \cdot e^{t^2}\)
Vi ricordate quando nella prima parte ho scritto che i diagrammi di fase si usano per i sistemi di ODE? Beh questo non è vero in forma assoluta, perché anche una singola ODE, se accompagnata da una condizione iniziale, produce una curva ben definita nel piano \((y,t)\). Ed è proprio quello che sto facendo qui. Ma perché in questo caso riusciamo? Semplicemente perché ora abbiamo un problema di Cauchy e non una ODE semplice. Avendo quindi una condizione iniziale, posso ricavarmi in valore di \(K\) e vedere l'andamento della \(y\) nel tempo con \(K\) noto. Quindi il campo di direzione ci mostra tutte le soluzioni possibili: il valore iniziale fissa quale tra queste la nostra
seguirà. Nel nostro caso la condizione iniziale è \(y(0) = 0\) che implica \(K=\frac{1}{2}\). Nel grafico, questo caso in particolare è rappresentato dalla linea verde (e no, non mettete su RAI 1). Anche qui, come nel caso precedente, abbiamo tre famiglie differenti:
- \(y > -\frac{1}{2}\): Le linee di campo decrescono molto velocemente (vedi la pendenza delle frecce) e poi tornano a crescere
- \(y < -\frac{1}{2}\): Le linee di campo crescono molto velocemente e poi tornano a decrescere
- \(y = -\frac{1}{2}\): La funzione rimane costante con valore nullo
Se volete verificare da voi, vi invito a porre come condizione iniziale \(y(0) = -\frac{1}{2}\) e a farvi i calcoli. Vedrete che implica \(K=0\).
Conclusioni
Giuro che ero partito con le migliori intenzioni, ma mi sono lasciato prendere la mano. Per cui eccoci qui, giunti alla fine di una seconda parte matematicamente abbastanza impegnativa. La terza parte, a questo punto, non vi prometto che lo sarà meno ma siete in ballo quindi ora BALLATE! Come al solito, eccovi il link al repo. Ah e se non si fosse capito, nel prossimo articolo della nostra amata serie, parlerò dei metodi numerici.
Alla Prossima.

