C'è un momento nella vita di ogni matematico, ingegnere e figure mitologiche simili, in cui
Ti piace l'analitica eh!? Allora beccati sta ODE.
E te ne sbatte in faccia una non lineare, accoppiata, implicita, con coefficienti che cambiano neanche fossero le scale di Hogwarts. L'unica cosa che puoi farci è non risolverla. Nemmeno pregando le buon anime di Gauss, Leibniz e altri matematici che veneri. O meglio questo era vero fino alla nascita dei metodi numerici. Poco eleganti, spesso sporchi, ma tremendamente efficaci. Non ti danno formule chiuse con cui vantarti, ma se ti accontenti del risultato approssimato non hai proprio di che lamentarti. Del resto, anche se non si direbbe, siamo circondati da approssimazioni: quando usate Google Maps (che vi dice che arriverete tra 10 minuti e ce ne mettete 17), quando mettete un pizzico di sale (dove il "pizzico" è un cucchiaio da cucina), quando leggete il mio blog (che dovrebbe essere divulgativo invece aiuta più me a ricordare che voi a imparare)...
Ma bando agli indugi, dato che non state più nella pelle vediamo questi famosi metodi numerici. Ma prima, se non l'hai fatto, recupera la Parte 1 e la Parte 2.
ODE a Piccoli Passi
Riprendiamo il tanto decantato sistema di Lotka-Volterra introdotto qui.
dove:
- \(x(t)\) è il numero di prede (es. conigli).
- \(y(t)\) è il numero di predatori (es. volpi).
- \(\alpha\) è il tasso di crescita delle prede. Descrive quanto velocemente si riproducono le prede in assenza di predatori (che nei conigli sembra essere alto come vuole la leggenda).
- \(\beta\) è il tasso di predazione. Dice quanto le prede vengono uccise dai predatori.
- \(\delta\) è il tasso di conversione. Dice quanti nuovi predatori nascono ad ogni preda mangiata e digerita.
- \(\gamma\) è il tasso di mortalità dei predatori. Rappresenta la morte naturale dei predatori in assenza di prede. Se non mangiano muoiono di fame.
Non c'è un metodo analitico noto per risolvere simbolicamente questo sistema quindi ricorriamo ai metodi numerici. Sono strategie per ottenere una soluzione approssimata, per passi piccoli, discreti e speranzosi. Tutto nasce grazie al sommo Eulero che, oltre a regalarci il famosissimo tatuaggio
(no serio ragà, smettete di tatuarvelo se non sapete manco cos’è il pi greco), ci ha dato anche il capostipite di tutti i metodi numerici: il metodo di Eulero. La convergenza di questo metodo è stata dimostrata dal sommo Cauchy ed è stato poi generalizzato dai sommi Runge e Kutta con la famiglia dei metodi RK. Insomma qui tutti sono sommi e il mondo dei metodi numerici è più affollato dell'algoritmo di TikTok. Ce ne sarebbero tanti altri da affrontare ma ci limiteremo solo ad alcuni.
Metodo Di Eulero
Riprendiamo la formula dell'espansione di Taylor. Ricordi? Ne ho già parlato qui. La serie di Taylor è un po' un jolly, si usa ovunque.
Consideriamo in particolare una espansione al primo ordine cioè del tipo
dove
cioè stiamo valutando la funzione in \(x\), considerando le derivate in un punto distante \(a\) da \(x\) stesso. Consideriamo ora un generico problema di Cauchy
e consideriamo la definizione di derivata. Possiamo scrivere, per \(h \rightarrow 0\):
Vi ricorda qualcosa? Esatto proprio uno sviluppo di Taylor al primo ordine ma dove:
- \(x = t + h\)
- \(a = t\)
Cioè calcoliamo la derivata nel punto \(t\) e valutiamo lo sviluppo nel punto \(t+h\). Ora facciamo un altro sforzo e supponiamo di partire dal punto \(t_0\) che è noto dato che, vi ricordo, siamo in un problema di Cauchy. Facciamo un passettino infinitesimo \(h\) in avanti e finiamo nel punto \(t_1\). Per cui scriviamo
dove
Una volta che conosciamo \(t_1\), possiamo andare in \(t_2\) con lo stesso principio
dove
Capita l'antifona? Possiamo quindi generalizzare in questo modo
Formula 1. Sviluppo della ODE di Ordine Uno
Quindi
Formula 2. Discretizzazione del Tempo
Dove:
- \(t_0\) è l'istante iniziale
- \(t_{n+1}\) è l'istante finale
- \(h\) è il passo di integrazione, scelto a piacere
- \(n\) è il numero di iterazioni
In pratica stiamo discretizzando il tempo. Più \(h\) è piccolo, più il metodo è accurato ma computazionalmente oneroso.
Riprendiamo ora il problema di Cauchy e abbiamo:
e quindi possiamo sostituire \(y'(t)\) nel metodo di Eulero, ottenendo la formulazione finale:
Formula 3. Metodo di Eulero Esplicito
Quella scritta è la formula del Metodo di Eulero Esplicito. Perché esplicito? Perché usiamo tutti valori che conosciamo già. Infatti supponiamo di voler calcolare \(y(t_1)\), dovremmo calcolare:
- \(y(t_0)\) che è il valore noto del problema di Cauchy
- \(f(y(t_0), t_0)\) calcolabile tramite semplice sostituzione di valori
Se esiste il metodo esplicito ovviamente esiste anche l'implicito la cui formula, omettendo la dimostrazione, è:
Formula 4. Metodo di Eulero Implicito
E' implicito perché, come potete vedere, il valore da calcolare \(t_{n+1}\) compare in entrambi i lati dell'equazione. Non sempre si risolve con facilità. In determinati casi, sono necessari metodi iterativi come il metodo delle sostituzioni successive. Ma questo esula questo articolo quindi, dato che la vita ce la siamo già complicati abbastanza, vi lascio alla vostra volontà di approfondire.
Esempio Eulero
Tutto troppo teorico fino ad ora lo so, quindi vediamo qualcosa di pratico con un esercizio. Consideriamo il seguente problema di Cauchy rappresentante il decadimento esponenziale. Sembra fine a se stesso, in realtà molti fenomeni naturali seguono questa legge come il decadimento radioattivo, la scarica del condensatore nei circuiti RC...
dove \(k\) è il tasso di decadimento e, in questo caso, lo scegliamo noi. La soluzione della ODE è:
Se volete i passaggi fateveli. Conoscete gli strumenti per risolverla. Per l'esempio ho scelto questa ODE (che è risolvibile analiticamente come avete visto), per poter mostrare la differenza tra una soluzione esatta e una numerica. Vediamo quanto vale nei punti \(t=1, \text{ } t=2\)
Ora risolviamo con il metodo di Eulero. Dalla formula di discretizzazione del tempo sappiamo già quanti sono gli step da fare posto \(h=0.1\), istante iniziale \(t_0=0\) e istante finale \(t_{n}=2\):
Per chiarezza di esposizione, eseguiamolo step by step. Il valore in \(t_0\) è noto dal problema di Cauchy, quindi:
- Passo \(n=1\)
$$ t_{1} = t_0 + 1 \cdot 0.1 = 0.1 $$
- Passo \(n=2\)
E così via. Fidatevi quando vi dico che i risultati sono quelli riportati in questa tabella:
Ora vediamo che succede ponendo \(h=0.5\). Non lo farò step by step perché ora sapete come si fa, quindi beccatevi sta tabella:
Ecco un confronto sintetico tra la soluzione analitica e le due approssimazioni numeriche:
- \(y(t)\) soluzione analitica
- \(E(h=0.1)\) Eulero con \(h=0.1\)
- \(E(h=0.5)\) Eulero con \(h=0.5\)
Come potete vedere, al netto di \(n=0\) che è la soluzione nota, \(h=0.1\) approssima molto meglio rispetto a \(h=0.5\) ma ha richiesto \(20\) passi rispetto ai \(4\) del secondo.
Quanto detto può essere riassunto dalla seguente immagine
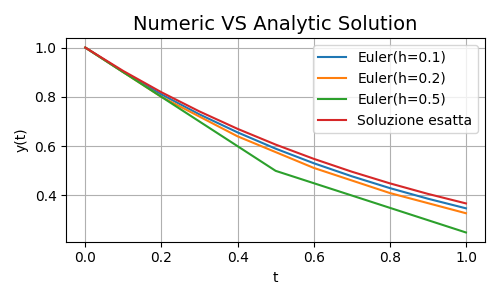 Figura 1. Comparazione Risultati
Figura 1. Comparazione Risultati
La soluzione esatta è quella rossa, e al diminuire di \(h\) l'approssimazione è via via migliore. Bene, è il momento di passare al prossimo round dove i Runge-Kutta vi stenderanno.
La Famiglia Mans... RK
Diamo a Cesare quel che è di Cesare, il metodo di Eulero è il patriarca di tutti i metodi numerici. Ma è davvero così buono? Beh come sempre... dipende. Ad esempio dal vostro tipo di problema. Per problemi troppo complessi fallisce miseramente. Quindi è buono e caro ma diciamocelo, non ha più l'età. C'è bisogno di carne fresca, di giovini pavidi e forti. Arriviamo così ai metodi Runge Kutta o RK.
I metodi RK sono una famiglia neocatecumenale, ce ne sono tanti, ed ognuno ha le sue peculiarità. L'unica cosa certa, oltre la morte, è che mantengono la stessa idea di base di Eulero. Procedere per piccoli passi.
Ripartiamo dalla formula di Taylor. Come ben ricorderete maggiore è lo sviluppo, migliore è l'approssimazione. I metodi RK si basano proprio sullo sviluppo di ordini superiori della serie di Taylor. Eulero quindi può essere visto come un metodo RK1 cioè Runge Kutta del primo ordine. Vediamo cosa succede se non ci accontentiamo del primo ordine ed arriviamo al secondo, partendo dalla Formula del Primo Ordine:
Dato che
Formula 5. Sviluppo della ODE di Ordine Due
Possiamo quindi utilizzare la definizione della derivata prima e sviluppare il rapporto incrementale di \(f'\):
Ma da Eulero sappiamo che
per cui, sostituendo:
Sostituendo ancora, nella formula dello Sviluppo di Ordine Due abbiamo:
Quindi posti:
troviamo il cosiddetto Metodo RK2 o Metodo di Heun
Formula 6. Metodo di Heun
Con la stessa logica, si possono calcolare ordini superiori sviluppando ulteriormente la serie di Taylor:
- RK3 o Shu-Osher
- RK4
- RK5 o Dormand-Prince
- ... e tanti altri.
Data la sua importanza, non si può non riportare la formulazione di RK4 che è un ottimo compromesso tra precisione e complessità computazionale:
Formula 7. Metodo RK4
Da notare che, sempre perché vi voglio bene, abbiamo considerato unicamente i metodi espliciti, ma solo perché abbiamo la testa sotto la sabbia non vuol dire che quelli impliciti (perché sì, esistono gli RK impliciti) non possano farvi del male.
Esempio RK
Se siete arrivati qui avrete sentito millanta volta Lotka-Volterra. Dato che ora possiamo, perché non risolverlo?! Consideriamo quindi la seguente istanza:
ovviamente, data tutta la paturnia sopra, usiamo i metodi numerici con
in particolare sviluppiamo per Heun e RK4. Tranquilli, è giusto per farvi vedere come funzionano quindi svilupperemo solo per un passo.
- Heun, \(n=1\)
Vi ricordo che Lotka-Volterra è un sistema di due ODE, quindi la faccenda si complica un pochino ma nulla di astruso, niente panico. Iniziamo calcolando \(k_1\) e \(k_2\). Dato che le ODE sono due, sono calcoleremo
- \(k_1^x, k_2^x\) per la prima ODE
- \(k_1^y, k_2^y\) per la seconda ODE
Sostituendo:
I più attenti di voi si chiederanno perché \(t+h\), che è richiesto per il calcolo di \(k_2\), di fatto non appare mai. Presto detto, tutte le ODE del sistema, non dipendono esplicitamente dalla variabile tempo \(t\), quindi è ininfluente ai fini del calcolo; ma se fosse apparso, il tempo corrente è quello calcolato tramite la Formula di Discretizzazione del Tempo mostrata nel paragrafo precedente.
- RK4, \(n=1\)
Per lo stesso principio di prima, calcoliamo:
- \(k_1^x, k_2^x, k_3^x, k_4^x\) per la prima ODE
- \(k_1^y, k_2^y, k_3^y, k_4^y\) per la seconda ODE
Sostituendo:
Si lo so, è una palla infinita e sembra chissà quale cosa complessa, ma in realtà una volta arrivati alla formulazione del metodo, si tratta solo di fare attenzione ad effettuare le sostituzioni giuste.
Così come fatto per il metodo di Eulero, portiamo anche qui una tabella di confronto. Ma questa volta non dividiamo per \(h\), bensì per metodo, e confrontiamo i risultati dei metodi RK4, Heun e Eulero. Per l'ennesima volta, dato che non possiamo calcolare la soluzione analitica, non possiamo avere il valore esatto ma solo gli approssimati.
Come si può vedere dalla tabella, Heun e RK4 danno risultati molto simili e si hanno delle variazioni solo dopo \(t=2\) secondi, mentre Eulero già dal secondo \(t=0.1\) inizia ad approssimare male. Nell'immagine che segue potete vedere l'andamento di fase.
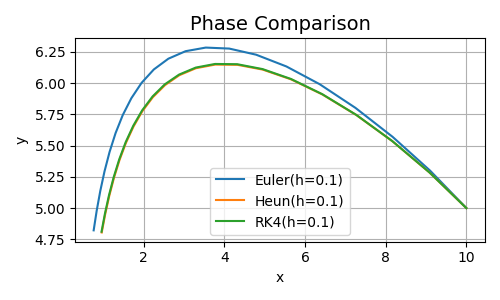 Figura 2. Comparazione Risultati per \(t=2\)
Figura 2. Comparazione Risultati per \(t=2\)
Vediamo infine cosa succede passando da \(t=2\) a \(t=15\).
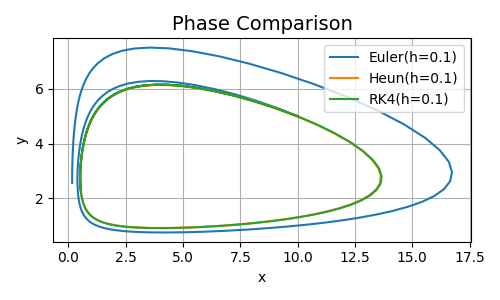 Figura 3. Comparazione Risultati per \(t=15\)
Figura 3. Comparazione Risultati per \(t=15\)
Come si nota, mentre Heun e RK4 hanno un andamento molto simile e coerente con la teoria creando una orbita chiusa (leggete i predenti articoli se non ricordate a cosa mi riferisco), l'errore che Eulero accumula e continua ad accumulare, è talmente grande che l'andamento della soluzione prende una strada tutta sua.
Per completezza vediamo anche l'andamento di prede e predatori, cioè di \(x\) e \(y\), rispetto al tempo \(t\)
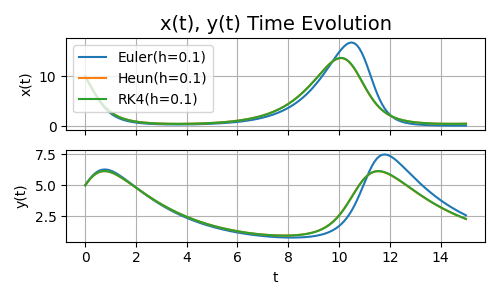 Figura 4. Andamento di \(x\) e \(y\) rispetto al tempo \(t=15\)
Figura 4. Andamento di \(x\) e \(y\) rispetto al tempo \(t=15\)
Conclusioni
Eccoci giunti alla fine di questo terzo articolo. Arrivati a questo punto dovreste sapere (o quanto meno ricordare per chi già aveva conoscenza), cosa sono derivate, integrali, equazioni differenziali e metodi numerici. E ci sarebbe tantissimo altro da dire, ho cercato di essere sintetico. Non c'è bisogno che mi ringraziate. In ogni caso, ora abbiamo tutti gli ingredienti per parlare delle Neural ODE. E se ve lo steste sì, anche lì ci sarà molta matematica. Concludo come sempre con il link al repo per vedere, in codice, quanto detto.
Alla Prossima.

