Dai che ci siamo. Siamo arrivati alla quinta e ultima parte della serie sulle NODE. Prendete questa affermazione con le pinze però, che se non mi basta questo spazio vi beccate anche la sesta. In ogni caso in questa (spero) ultima parte, vedremo un po' di codice e di applicazione di una NODE. Prima di iniziare, se siete giunti a questa pagina senza aver letto le precedenti, vi consiglio vivamente di recuperarle. Qui trovate i link agli articoli precedenti. Detto questo senza perdere altro tempo, iniziamo.
Dal NODE al Code
Se c'è una cosa che abbiamo imparato (o almeno avremmo dovuto), è che di fatto le NODE si differenziano dalle reti normali non tanto a livello architetturale, quanto nell'utilizzo che si fa di queste architetture. In virtù di ciò, non facciamo i razzisti. Non trattiamo le NODE diversamente. Sono in grado di fare tutto quello che fà una rete neurale classica. Si possono utilizzare per problemi di classificazione, di regressione e anche di generazione. Va da sè che data la loro natura continua, si prestano bene per determinati use case e non per tutti. Poi, ciò non toglie che potete utilizzare quando, come e perché volete. Non sarò di certo io a impedirvelo. Negli esempi che mostrerò le utilizzerò nel loro habitat naturale, il forecasting, e comparerò i risultati con quelli prodotti da una rete neurale classica.
(Ancora) Lotka-Volterra
Iniziamo da questo primo use case. Supponiamo di avere una Time Series, la cui natura ci è ignota. Sappiamo solo che abbiamo numeri buttati in una lista. Noi sappiamo che numeri sono ma acqua in bocca, la NODE non ne ha idea di cosa rappresentano. Ecco questa lista di numeri rappresenta la nostra base di partenza. I dati sui quali andremo ad addestrare la nostra NODE. Dato che, malauguratamente, questi dati non si generano da soli, dobbiamo crearli noi. Se vi state chiedendo come, niente di più semplice. Prendiamo il nostro bel modellino dinamico di Lotka-Volterra e diamolo in pasto ad un ODESolver. Se non sapete come è definito, recuperate la parte 3.
Ma basta parlare, mostriamo un po' di codice e creiamo una classe LotkaVolterra che estende un generico DatasetProvider,
dove definiamo la dinamica del sistema e come generare i dati.
Creazione Del Dataset
class LotkaVolterra(DatasetProvider):
def __init__(self, n_train: int = 80, noise_std: float = 0.01,
t_train_range: tuple[float, float] = (0.0, 6.0),
t_extra_range: tuple[float, float] = (6.0, 10.0),
n_extra: int = 200, n_resamp: int = 200,
alpha: float = 1.5, beta: float = 1.0,
delta: float = 0.75, gamma: float = 1.0,
initial_values: tuple[float, float] = (2.0, 1.0)) -> None:
super().__init__(initial_values=initial_values, n_train=n_train, noise_std=noise_std,
t_train_range=t_train_range, t_extra_range=t_extra_range, n_extra=n_extra,
n_resamp=n_resamp)
self.alpha = float(alpha)
self.beta = float(beta)
self.delta = float(delta)
self.gamma = float(gamma)
...
def dynamics(self, t: torch.Tensor, state: torch.Tensor) -> torch.Tensor:
x1, x2 = state[0], state[1]
x1dt = self.alpha * x1 - self.beta * x1 * x2
x2dt = self.delta * x1 * x2 - self.gamma * x2
return torch.stack([x1dt, x2dt]).to(self.dtype)
def _solve_at(self, t_grid_np: np.ndarray, method: str, dynamics: Callable) -> np.ndarray:
...
sol = odeint(dynamics, self.x0_t, t_tensor, method=method, rtol=self.r_tol, atol=self.a_tol)
...
return sol
def __call__(self, method: str, dynamics: Callable) -> DataObject:
t_train = np.sort(rng.uniform(*self.t_train_range, size=self.n_train))
x_train_true = self._solve_at(t_grid_np=t_train, method=method, dynamics=dynamics)
x_train_noised = x_train_true + self.noise_std * rng.standard_normal(x_train_true.shape)
t_test_extra = np.linspace(*self.t_extra_range, self.n_extra)
x_test_extra_true = self._solve_at(t_grid_np=t_test_extra, method=method, dynamics=dynamics)
t_test_resamp = np.sort(rng.uniform(*self.t_train_range, size=self.n_resamp))
x_test_resamp_true = self._solve_at(t_grid_np=t_test_resamp, method=method, dynamics=dynamics)
x_test_resamp_noised = x_test_resamp_true + self.noise_std * rng.standard_normal(x_test_resamp_true.shape)
return self._create_dict(t_train, x_train_noised, x_train_true, t_test_extra, x_test_extra_true, t_test_resamp, x_test_resamp_true, x_test_resamp_noised)
def prepare_data(self, data: DataObject, shuffle: bool = True, use_noise: bool = True, train_K_max: Optional[int] = None) -> Loaders:
out = {}
if train_K_max is None:
ds_train = self._build_pairwise_transitions(data["t_train"], data["x_train_noised" if use_noise else "x_train_true"],
data["x_train_true"], device=device)
else:
ds_train = self._build_multi_horizon_transitions(data["t_train"], data["x_train_noised" if use_noise else "x_train_true"],
data["x_train_true"], K_max=train_K_max, device=device)
out["train"] = {"dataset": DataLoader(ds_train, batch_size=batch_size, shuffle=shuffle)}
ds_resamp = self._build_pairwise_transitions(data["t_test_resamp"], data["x_test_resamp_noised" if use_noise else "x_test_resamp_true"], data["x_test_resamp_true"], device=device)
out["resamp"] = {"dataset": DataLoader(ds_resamp, batch_size=batch_size, shuffle=False)}
ds_extra = self._build_pairwise_transitions(data["t_test_extra"], data["x_test_extra_true"], data["x_test_extra_true"], device=device)
out["extra"] = {"dataset": DataLoader(ds_extra, batch_size=batch_size, shuffle=False)}
return out
Si lo sò, è tanto codice. Ma lasciate che ve lo spieghi. Nel costruttore, oltre a passare i parametri necessari alla definizione del sistema, forniamo anche informazioni relative a come vogliamo che venga costruito il nostro dataset:
t_train_range: Rappresenta il range temporale nel quale vogliamo che siano presi i campioni di train e di test.n_train: Indica il numero di campioni di train che vogliamo generare.n_resamp: Indica il numero di campioni di test che vogliamo generare.noise_std: Serve a sporcare i dati di train e di test. Perché che vita sarebbe senza un po' di difficoltà?t_extra_range: Rappresenta il range temporale del quale vogliamo fare forecast.n_extra: Indica il numero di campioni che si vogliono prevedere nel range di forecast.
Quindi se consideriamo le seguenti righe:
DataCreator = LotkaVolterra
params = {
"n_train": 350,
"noise_std": 0.01,
"t_train_range": (0.0, 12.0),
"t_extra_range": (12.0, 18.0),
"n_extra": 300,
"n_resamp": 200,
}
data_creator = DataCreator(**params)
data = data_creator.prepare_data(data)
quello che stiamo chiedendo è di avere un dataset composto da:
- \(350\) samples di train campionati casualmente nel range temporale \((0, 12)\) secondi, ed i relativi istanti temporali.
- \(200\) samples di test campionati casualmente nel range temporale \((0, 12)\) secondi, ed i relativi istanti temporali.
- \(300\) samples di forecast nel range \((12, 18)\) secondi (utilizzati solo per verificare se le predizioni sono corrette), ed i relativi istanti temporali.
Questi dataset sono strutturati in questo modo:
idx t_i x_i t_next x_next dt
--------------------------------------------------------------------------------
0 0.023 [ 1.986 -0.044] 0.118 [ 1.986 -0.235] 0.095
1 0.118 [ 1.968 -0.245] 0.159 [ 1.975 -0.314] 0.041
2 0.159 [ 1.986 -0.314] 0.160 [ 1.975 -0.317] 0.001
3 0.160 [ 1.971 -0.318] 0.200 [ 1.96 -0.394] 0.040
4 0.200 [ 1.988 -0.383] 0.211 [ 1.956 -0.415] 0.011
5 0.211 [ 1.948 -0.398] 0.306 [ 1.908 -0.593] 0.094
... ... ... ... ... ...
dove:
- \(t_i\): E' l'attuale istante temporale.
- \(x_i\): E' lo stato nell'istante attuale, calcolato sia con l'aggiunta di rumore che senza, nel caso di
trainetest. - \(t_{next}\): E' l'istante temporale successivo.
- \(x_{next}\): E' lo stato nell'istante temporale successivo. Nel caso di
train, lo stato è il valore a \(K\) passi di distanza, con \(K\) intero casuale. - \(dt\): E' il delta trascorso dai due istanti temporali.
Facendo il plot di questi dati otteniamo l'immagine che segue:
Figura 1. Dataset di Train Vero e Rumoroso
Se vi steste chiedendo come, di fatto, risolviamo la dinamica, lo facciamo tramite il metodo odeint definito dalla libreria torchdiffeq,
che fornisce metodi di alto livello per la gestione delle NODE. Questo metodo implementa vari ODESolver,
e nel nostro caso è stato utilizzato dopri5
Definizione Delle Reti
Dato che l'obiettivo principale è comparare i risultati a parità di condizioni, si sono utilizzate due reti quasi identiche. Andiamo a vedere perché sono quasi identiche e non identiche.
def lotka_volterra_nets():
def create_net(is_node: bool):
input_dim = LotkaVolterra.get_dim() if is_node else LotkaVolterra.get_dim() + 1
return nn.Sequential(
torch.nn.Linear(input_dim, 16),
torch.nn.Tanh(),
torch.nn.Linear(16, 32),
torch.nn.Tanh(),
torch.nn.Linear(32, LotkaVolterra.get_dim()),
)
class SimpleNet(nn.Module):
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
self.ann = create_net(is_node=False)
self.name = LotkaVolterra.get_name() + "_MLP"
def forward(self, x, dt):
z = torch.cat([x, dt], dim=-1)
return self.ann(z)
class NODE(nn.Module):
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
self.ann = create_net(is_node=True)
self.method = LotkaVolterra.get_method()
self.name = LotkaVolterra.get_name() + "_NODE"
self.h = 0.01
def forward(self, t, state):
return self.ann(state)
return SimpleNet(), NODE()
Mentre per le NODE, l'utilizzo del tempo \(t\) è implicito nella loro natura, questo non è vero per le reti classiche.
Quindi per queste ultime, dobbiamo considerare esplicitamente il fattore tempo e lo facciamo considerandolo come feature aggiuntiva. Per via di ciò la rete neurale classica, che chiamiamo
SimpleNet ha una dimensione in più in input.
La NODE invece, accetta il parametro \(t\) in fase di forward ma viene utilizzato per il calcolo della dinamica e non
come feature in maniera diretta. Quindi è necessario passarlo, ma non incide sul numero di neuroni, che rimangono pari al numero di variabili del problema. Avendo quindi
due architetture quasi uguali ma non identiche, mi sono dovuto accontentare di avere due inizializzazioni diverse dei pesi, ahimè non si può avere tutto nella vita. Ma almeno la
salute c'è (per ora). Ultima nota. No non sono impazzito, se ho utilizzato le Tanh come funzioni di attivazione è perché torchdiffeq specifica di evitare
l'utilizzo di attivazioni non smooth.
Ora che abbiamo due modelli pronti e un dataset su cui metterli alla prova, passiamo finalmente all’addestramento.
Addestramento
Essendo le reti di natura diversa, lo sarà anche il train. Ad alto livello neanche troppo a dire la verità ma a basso livello beh...leggetevi la quarta parte e la serie di articoli sui neuroni per capire quanto in realtà siano profondamente diversi. Dato che, fortunatamente, qualcuno ha già smazzato il lavoro sporco per noi, questa differenza ad alto livello si nota ben poco. Andiamola a vedere:
def train_mlp(model, train_loader, resamp_loader):
...
for i in range(start_epoch, start_epoch + epochs):
model.train()
epoch_loss = 0.0
for x_i, x_next, dt, t_i, t_next in train_loader:
opt.zero_grad()
y = model(x_i, dt)
loss = crit(y, x_next)
loss.backward()
opt.step()
epoch_loss += loss.item() * (x_i.shape[0] if x_i.ndim > 1 else 1)
train_avg = epoch_loss / len(train_loader.dataset)
val_avg = eval_mlp(loader=resamp_loader, model=model)
...
def train_node(model, train_loader, resamp_loader):
...
for epoch in range(start_epoch, start_epoch + epochs):
model.train()
epoch_loss = 0.0
for x_i, x_next, _dt, t_i, t_next in train_loader:
opt.zero_grad()
preds = []
for j in range(x_i.size(0)):
tspan = torch.stack((t_i[j], t_next[j])).to(device=x_i.device, dtype=x_i.dtype)
x_T = odeint(model, x_i[j], tspan)[-1]
preds.append(x_T)
y = torch.stack(preds, 0)
loss = crit(y, x_next)
loss.backward()
opt.step()
epoch_loss += loss.item() * (x_i.shape[0] if x_i.ndim > 1 else 1)
train_avg = epoch_loss / len(train_loader.dataset)
val_avg = eval_node(model=model, loader=resamp_loader)
...
Come si può vedere, quando andiamo ad addestrare SimpleNet attraverso la funzione train_mlp, forniamo i dati in batch. Questo perché nel suo utilizzo classico, la rete neurale può gestirlo. Per cui quello che facciamo
è fornire in batch, alla rete, delle coppie \((x_i, dt)\). La generica predizione \(y\) della rete, ottenuta per ogni coppia, rappresenta quanto varrà lo stato di input \(x_i\),
trascorsi \(dt\) secondi. La loss, che è una MSE, viene calcolata usando lo stato predetto \(y\) e lo stato di arrivo vero \(x_{next}\).
Per quanto riguarda NODE invece, come si può vedere, usa al suo interno il metodo odeint ma questa volta non forniamo una ODE rappresentante la dinamica, bensì la rete neurale
stessa, e lo scopo è far si che impari la dinamica a partire dai dati, e quindi fare la corretta previsione di come evolverà il sistema. Mentre nelle SimpleNet la differenza temporale era fornita
e quindi si possono gestire i batch, qui questo concetto viene meno. Questo perché il tempo è implicito nelle NODE come detto, ma odeint lavora con un solo range temporale la volta, mentre
per ogni \(x_i\) del dataset, il \(dt\) cambia. Quindi quello che avviene ciclicamente nel train è questo:
- Prendiamo lo stato \(x_i\) come stato iniziale.
- Prendiamo l'istante temporale \(t_i\) associato allo stato \(x_i\).
- Prendiamo l'istante finale \(t_{next}\) associato allo stato finale \(x_{next}\).
- Integriamo tramite un ODESolver la dinamica \(f\) rappresentata dalla rete
NODEdall'istante iniziale \(t_i\) a quello finale \(t_{next}\), con condizione iniziale \(x_i\). - Prendiamo lo stato finale \(x_T\) che rappresenta il valore predetto.
Questi passaggi avvengono per tutti i campioni del dataset e, una volta completato il ciclo, calcoliamo la loss MSE usando stati predetti \(x_T\) e stati veri \(x_{next}\). Addestrando le reti con \(100\) epoche, l'output di questa fase è qualcosa del tipo:
Loading Dataset for LotkaVolterra
[ckpt] new best at epoch 0: train=3.042975, resamp=2.176756
Epoch 000 | train 3.042975 | resamp 2.176756
[ckpt] new best at epoch 1: train=1.603393, resamp=1.257801
Epoch 001 | train 1.603393 | resamp 1.257801
[ckpt] new best at epoch 2: train=0.689440, resamp=0.469525
Epoch 002 | train 0.689440 | resamp 0.469525
...
Epoch 099 | train 0.003902 | resamp 8.248611
MLP Train Done in 31.057s
...
[ckpt] new best at epoch 0: train=0.007876, resamp=0.563527
Epoch 000 | train 0.007876 | resamp 0.563527
[ckpt] new best at epoch 1: train=0.007059, resamp=0.510813
Epoch 001 | train 0.007059 | resamp 0.510813
Epoch 002 | train 0.006362 | resamp 0.537184
...
Epoch 099 | train 0.000170 | resamp 0.038154
NODE Train Done in 512.356s
Notiamo subito che la NODE ci ha messo non tanto, ma tantissimo di più rispetto la rete tradizionale. Se vi steste chiedendo il perché beh, non avete letto la quarta parte. Ma non fermiamoci solo ai numeri e vediamo con i nostri occhi come è andato il train. Ecco il risultato visivo del processo di addestramento per entrambi i modelli, riprodotto in tempo reale:
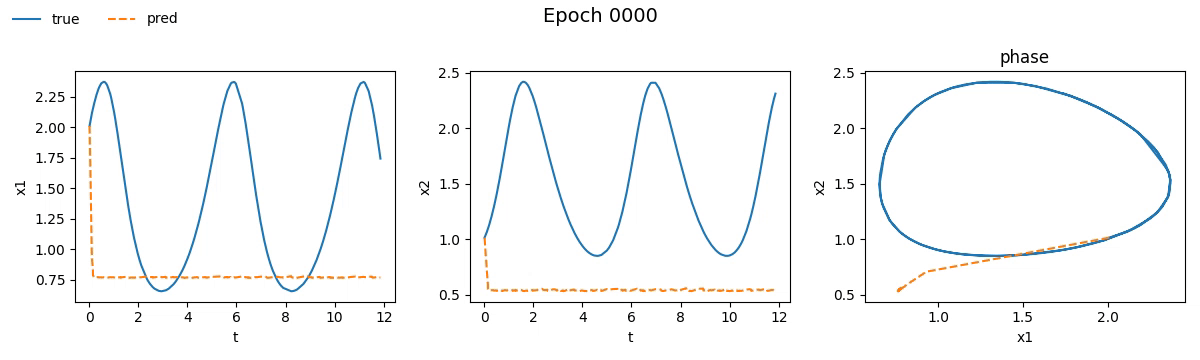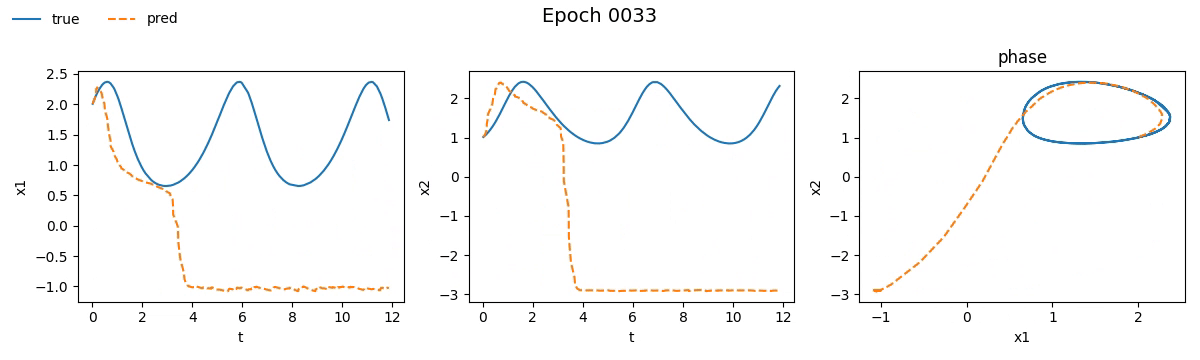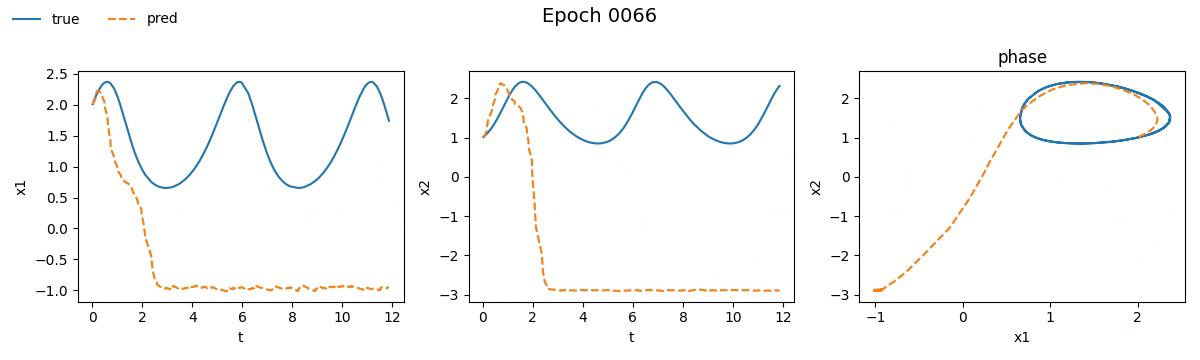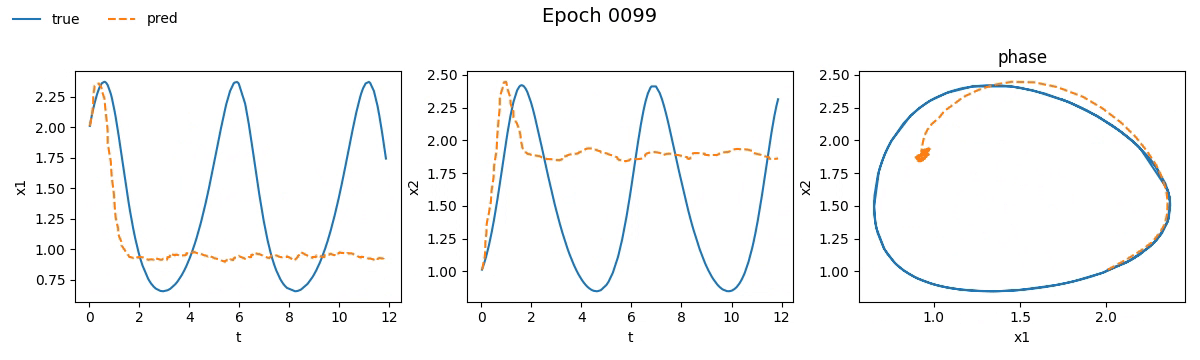Figura 2. Addestramento su Lotka-Volterra di SimpleNet
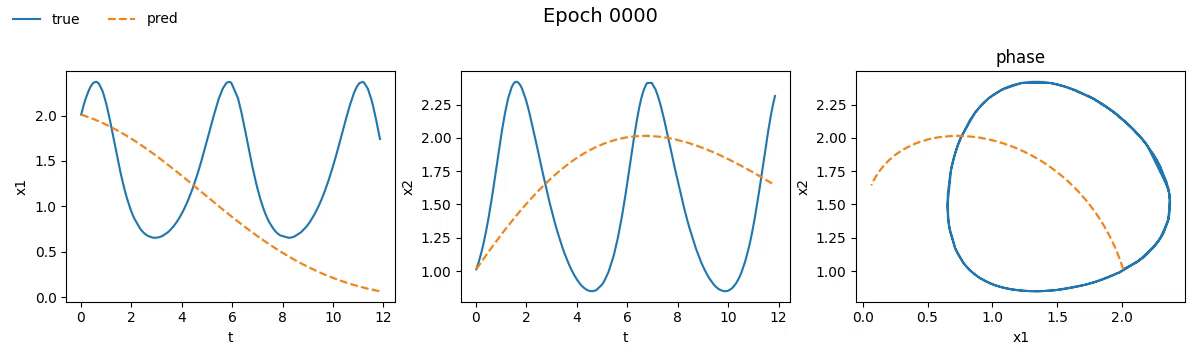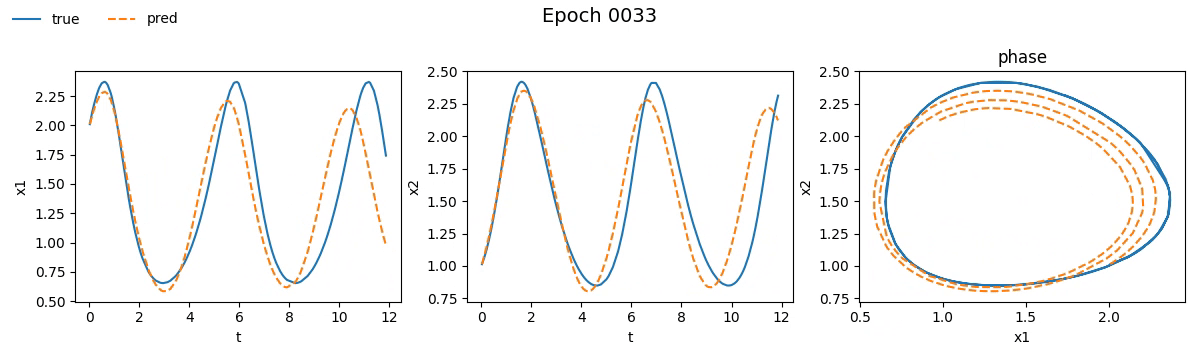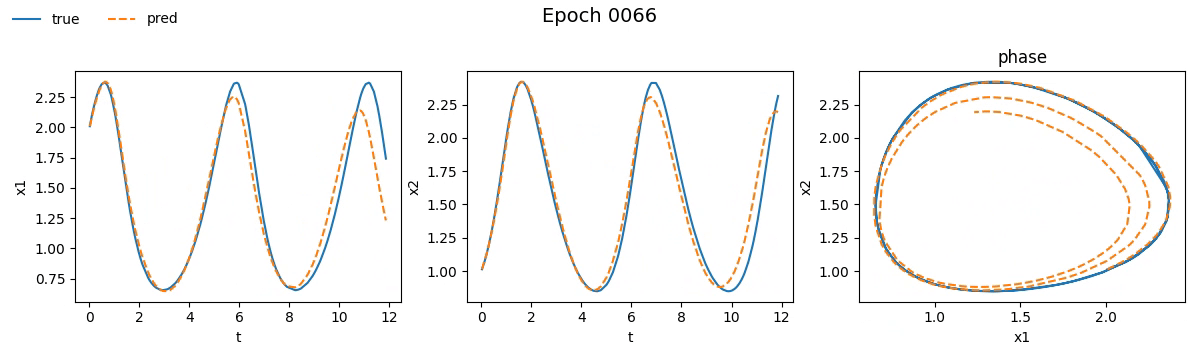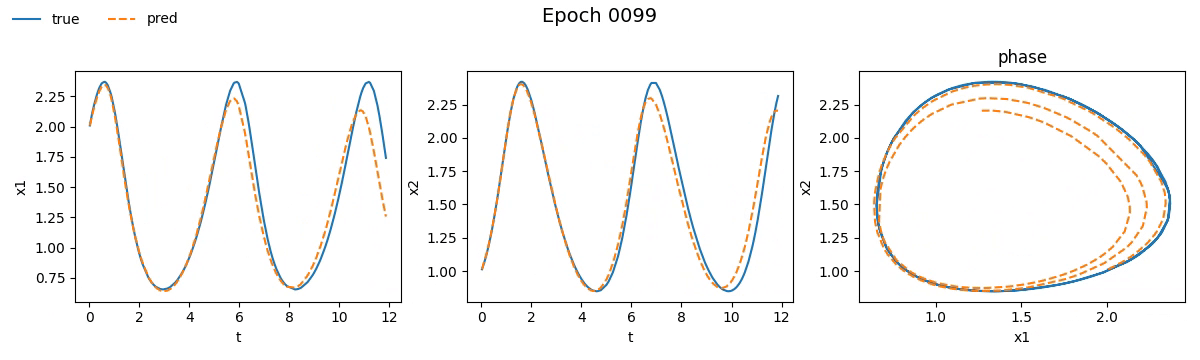Figura 3. Addestramento su Lotka-Volterra di NODE
Già da queste gif, si può vedere che con sole \(100\) epoche, la NODE sembra aver capito la dinamica molto meglio della SimpleNet.
Ma addestrare non basta. Vediamo ora come si comportano questi modelli quando li mettiamo alla prova fuori dal range di training.
Forecast
Nella fase di train abbiamo insegnato, o almeno ci abbiamo provato, alle reti NODE e SimpleNet a seguire l'andamento di un sistema dinamico.
Ok si, era il Lotka-Volterra, ma questo le reti non lo sanno. Quello che hanno visto è stato solamente una lista di valori campionati a caso nel tempo.
Ma come facciamo a verificare se effettivamente hanno capito? Per quel che ne sappiamo, potrebbero aver imparato benissimo il train e test set,
ma senza essere in grado di generalizzare. Quello che vogliamo è verificare che:
Dati i campioni da \((0, \, 12)\) secondi, riesco a prevedere l'andamento da \(12\) secondi in poi?
Per fare questo dobbiamo procedere in due modi differenti per SimpleNet e NODE. Questo perché mentre la predizione in avanti é implicita nelle NODE, non lo é per
le reti classiche. Per SimpleNet quindi, utilizziamo un approccio autoregressivo, cioé si sfrutta lo stato predetto come input per quantificare lo stato successivo.
Andiamo a vedere in codice cosa significa:
@torch.no_grad()
def predict_mlp(model, loader) -> tuple[np.ndarray, np.ndarray]:
...
x = x_i[0]
for k in range(t_grid.size(0)-1):
dt = t_grid[k+1]-t_grid[k]
x = model(x, dt)
traj.append(x)
pred = np.stack(traj, 0)
...
return pred, tgt
@torch.no_grad()
def predict_node(model, loader) -> tuple[np.ndarray, np.ndarray]:
...
x0 = x_i[0]
traj = odeint(model, x0, t_grid, method=model.method)
...
return traj, tgt
Nella funzione predict_mlp, utilizzata per fare le predizioni tramite SimpleNet, prendiamo un valore di partenza che può essere lo stato \(x\) in \(t=12\) secondi. Facciamo
la predizione usando come input \(x\) e andando in avanti di un tempo \(dt\). L'output, cioé lo stato al tempo \(dt\), viene utilizzato come input per fare la predizione dello
stato successivo al \(dt\) successivo. Dato che noi vogliamo fare predizioni nel range \((12, 18)\) secondi, questo ciclo continua fino ad arrivare a \(t=18\). Questo tipo di predizione iterativa però è
fragile: ogni errore si propaga nel tempo, rendendo più difficile una buona generalizzazione.
Per quanto riguarda la NODE invece, ci semplifica di molto le cose dato che proprio per la sua natura, quando andiamo a integrare da \(12\) a \(18\) secondi, stiamo calcolando la
dinamica e quindi tutti gli stati di quel range temporale. In pratica, è sufficiente chiamare odeint una sola volta con tutti i tempi nel range
desiderato, e il modello restituirà l'intera traiettoria prevista. Ma bando alle parole e vediamo come se la sono cavata le nostre reti a predire il futuro.
Figura 4. Forecast di Lotka-Volterra con SimpleNet
Figura 5. Forecast di Lotka-Volterra con NODE
Già dai video del train si poteva intuire che SimpleNet non era andata proprio egregiamente. E vedendo il forecast possiamo dire a cuore leggero che
non ha capito una fava e infatti il suo forecast é, a dir poco, osceno già dal secondo step. Vediamo che la NODE invece, sembra
aver capito molto bene la dinamica dato che riesce a fare una buona predizione di tutti gli stati su una finestra temporale molto ampia.
In conclusione, la NODE non solo ha dimostrato di adattarsi bene ai dati, ma ha saputo generalizzare su una finestra temporale mai vista. Certo, la NODE ci mette molto di più, ma come diceva qualcuno: la qualità ha il suo prezzo.
L'Oscillatore Armonico
Il secondo problema affrontato é quello dell'oscillatore armonico. Non rispiegherò tutti i passaggi dato che sono praticamente gli stessi visti sopra ma con dati diversi. In questo paragrafo mi limiterò a dire come sono passato da un problema fisico ad un modello matematico, e vedremo i soli risultati del forecast.
Partiamo dal classico esercizietto di fisica dove c'è una massa attaccata ad una molla, come nell'immagine che segue.
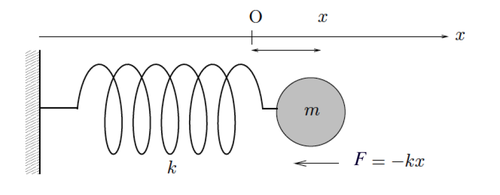Figura 6. Massa Attaccata ad una Molla
Se provaste a tirare e rilasciare la massa, quest'ultima oscillerebbe intorno al suo punto di equilibro fino a tornare alla situazione stabile in cui è fermo. Questo moto si chiama oscillatore armonico. Vediamone le leggi fisiche. Dalla legge di Newton sappiamo che una forza è pari alla massa per una accelerazione. Ma cosa è una accelerazione? Dalla parte 1 sappiamo che la velocità è la derivata prima dello spazio rispetto al tempo. Dato che l'accelerazione è la derivata prima della velocità rispetto al tempo, abbiamo di conseguenza, che l'accelerazione è la derivata seconda dello spazio rispetto al tempo. Nell'immagine in alto noi uno spazio lo abbiamo. E' la distanza tra la massa \(m\) e il suo punto di equilibrio, e nell'immagine è \(x\). Per cui scriviamo:
Ma dalla legge di Hooke sappiamo che la forza elastica è una forza opposta allo spostamento fatto che dipende dalla costante elastica \(k\) della molla e dallo spostamento stesso, per cui possiamo scrivere:
Quindi, se non ci sono altre forze in gioco, la forza totale è data dalla sola componente elastica. Per cui scriviamo:
Supponiamo che la massa posi su un pavimento di plastica che fa molto attrito. Per definizione una forza di attrito è pari alla velocità per un coefficiente di attrito. La velocità come abbiamo detto, è la derivata prima dello spazio rispetto al tempo. Inoltre, essendo una forza dissipativa, sottrae energia al sistema. Quindi scriviamo:
Considerando anche questa forza in tutto il sistema, abbiamo:
Da cui
Ponendo:
Dove \(\omega^2\) è chiamato frequenza naturale dell'oscillatore e \(\gamma\) coefficiente di smorzamento. Quindi:
Siamo arrivati alla forma differenziale dell'oscillatore armonico. Ma ancora non abbiamo finito, perché gli ODESolver lavorano solo con equazioni differenziali di primo grado, quindi cosi come é non sappiamo cosa farcene. Allora scomodiamo una proprietà delle equazioni differenziali, in particolare quella che dice che:
Ogni equazione differenziale ordinaria di ordine \(n\), può essere riscritta come un sistema equivalente di \(n\) equazioni del primo ordine.
Facciamo quindi un semplice cambio di variabile e poniamo:
Dopo questo cambio di variabili possiamo scrivere la precedente equazione differenziale di ordine due, in due equazioni differenziali del primo ordine:
Questa è una forma che un ODESolver può risolvere e rappresenta la nostra dinamica da risolvere. In termini di codice questa dinamica diventa:
class HarmonicOscillator(DatasetProvider):
def __init__(self, n_train: int = 80, noise_std: float = 0.01, t_train_range: tuple[float, float] = (0.0, 10.0),
t_extra_range: tuple[float, float] = (10.0, 15.0), n_extra: int = 200, n_resamp: int = 200, omega: float = 1.0,
gamma: float = 0.1, initial_values: tuple[float, float] = (2.0, 0.0)) -> None:
super().__init__(initial_values=initial_values, n_train=n_train, noise_std=noise_std,
t_train_range=t_train_range, t_extra_range=t_extra_range, n_extra=n_extra,
n_resamp=n_resamp)
self.omega = float(omega)
self.gamma = float(gamma)
...
def dynamics(self, t: torch.Tensor, state: torch.Tensor) -> torch.Tensor:
x1, x2 = state[0], state[1]
x1dt = x2
x2dt = -(self.omega ** 2) * x1 - self.gamma * x2
return torch.stack([x1dt, x2dt])
...
Il resto, come si suol dire, è storia. Per cui mi limito a riportare i grafici del forecast:
Figura 7. Forecast dell'Oscillatore Armonico con SimpleNet
Figura 8. Forecast dell'Oscillatore Armonico con NODE
Da questi grafici possiamo vedere come, ancora una volta, la NODE sembra aver compreso la dinamica mentre la rete classica la si nota un pochino confusa.
Insomma per tirare le somme, le NODE hanno dimostrato il loro potenziale, soprattutto in contesti dove c'è dinamica continua.
Sono lente? Sì.
Sono pesanti da integrare? Pure.
Sono difficile da tunare? Anche.
Ma sanno imparare come si evolve un sistema, e sanno farlo bene. Con occupazione spaziale costante, architetture più semplici e una spiccata capacità di generalizzazione.
Conclusioni
Chiudiamo, finalmente, questa serie di articoli sulle NODE. E' stato un viaggio lungo e, diciamocelo, faticoso. Sia per me che per voi. Però dai, ci portiamo a casa un bel bagaglio, no? Prima di concludere, ci terrei a mettere i puntini sulle i su un paio di aspetti. Partiamo dalle reti classiche, che qui sembrano un pò bistrattate. In realtà non è così. Per mantenere il confronto equo ho usato un solo approccio di train, ma con le giuste attenzioni anche una rete classica può cavarsela egregiamente. L'altro punto da sollevare è sulle NODE. Ho finito la serie di articoli, è vero, ma le NODE sono solo la base. Coloro che hanno dato il via. Qui le ho utilizzate per fare forecast ma, esattamente come le reti classiche, si possono usare per classificazione, regressione, generazione... E non solo: dalle NODE nascono tante altre architetture interessanti. Dai CNF per la generazione di immagini, alle Liquid Neural Network per robotica e controllo, fino alle Physics Informed Neural Network (Reti Lagrangiane, Reti Hamiltoniane, ...) reti che incorporano la fisica per modellare fenomeni complessi. Insomma, chi più ne ha più ne metta. E ognuna di queste architetture merita una dissertazione a parte. Chissà, magari un giorno ve la propinerò.
Detto questo, vi invito come sempre a leggere il codice completo qui e anche a lanciarlo voi stessi.
Alla Prossima.