Crystal Structure Algorithm

For my first article, I’d like to talk about a topic that’s very close to my heart: Metaheuristics. Despite the name, it’s not some ancient Assyrian demon, but rather a family of algorithms designed to solve computational and optimization problems — that is, problems involving finding a maximum or minimum.

When we face very large or complex problems — such as NP-Complete problems — finding the perfect solution would take an impractically long time.
And that’s where metaheuristics come into play. These algorithms don’t promise the absolute optimum, but they do their best to find very good solutions within a reasonable time, often using approaches inspired by nature and its processes. Just think of ACO, which is based on the behavior of ants, or PSO, inspired by the movement of swarms.

Among the many metaheuristic algorithms, one in particular caught my attention — both for its elegance and for the originality of its inspiration: the Crystal Structure Algorithm, or CryStAl.

This algorithm is inspired by the formation processes of crystal structures, where elements — atoms, molecules, or ions — arrange themselves in an orderly and symmetrical way, as seen in quartz crystals, for example.

CryStAl stands out for a particularly interesting feature: it is a parameter-free algorithm. Unlike many other approaches, it doesn't require manually setting values to control the optimization behavior. Instead, it manages the balance between exploration (searching for new solutions in different areas) and exploitation (refining already promising solutions) on its own, adapting dynamically throughout the process.
At the core of the algorithm are four distinct phases of solution updating, which allow it to effectively combine local search (improving solutions near those already found) and global search (exploring new areas in the solution space).

Where the Idea Comes From

Solid minerals whose components are arranged in a regular and repeated pattern along all three spatial dimensions are called crystals. At the heart of this orderly structure lies the lattice — a kind of three-dimensional grid made up of points, which repeats through space.
By itself, though, the lattice doesn’t tell us exactly where the atoms are. That’s where another piece of the puzzle comes in: the basis, meaning the set of atoms that repeats at each point of the lattice. In other words: the lattice tells us where to place something, the basis tells us what goes there and how it’s oriented in space. Here’s an example using blue dots and gummy bears.

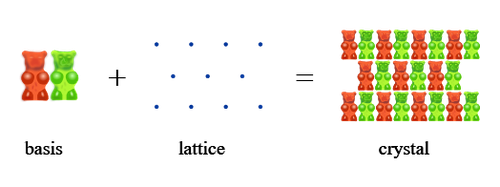Figure 1. Basis + Lattice

Thanks to the concepts of lattice and basis, it’s possible to generate an infinite number of crystal structures. The lattice, with its regular arrangement of points, defines the overall shape of the crystal, while the basis — that is, the repeating set of atoms — determines its internal configuration. By combining these two elements in different ways, we can obtain crystals with a wide range of geometries, some regular and well-known, others more complex. Below are a few examples of how these structures can vary:

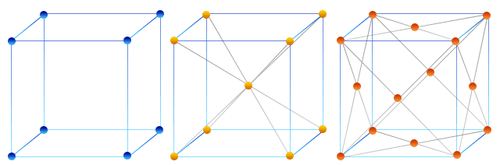Figure 2. Examples of Cubicle Crystals

The lattice, together with its basis, is the ordered and ideal structure that our artificial crystals — as we’ll soon see — will have to try to replicate during optimization.

The Mathematical Model

The mathematical model used by the authors of this algorithm is the Bravais lattice model, which allows the description of all possible lattices that can exist in three-dimensional space.
Each point in the lattice can be reached starting from the origin and taking an integer number of steps along each of the three directions: right|left, forward|backward, up|down. A position vector is then defined using the following formula:

\(\overrightarrow{r} = \sum_{i=1}^{d}n_i \overrightarrow{a_i}\) Where:

• \(d\) is the number of dimensions of the crystal, which is usually 3 (unless you live in a world with 4 spatial dimensions — in that case, please invite me over).
• \(n_i\) is an integer indicating how many steps we take along the direction \(a_i\).
• \(a_i\) represents the "movement direction".

Now that we’ve defined \(\overrightarrow{r}\), let’s set it aside for now — but don’t worry, it’ll be back soon. May Thor strike me down if I ever make you give up your beloved \(\overrightarrow{r}\).

Let’s get back to it and take a look at the candidate solutions. That’s right: in metaheuristic algorithms, there isn’t just one solution, but a whole set of candidate solutions, from which we’ll select the best one... Ahem, I mean — each candidate solution (or "crystal") is represented as a numerical vector in \(d\) dimensions, that is, a list of values:

\(C_i = \left[x_{i}^{1}, x_{i}^{2}, \dots, x_{i}^{d} \right]\)

Where:

• \(C_i\) is the \(i\)-th crystal.
• Each \(x_{i}^{j}\) indicates the value of the \(j\)-th variable in crystal \(i\).

So the crystal population is defined as:

In other words, we have a population of \(n\) crystals, each with \(d\) variables. This matrix — where each row is a crystal and each column is a variable — represents the entire search space from which the algorithm will try to extract the best candidate.

Alright, all clear so far (I hope)! But now the question is... How the heck do we create these crystals?
Simple as that.
Given a fitness function \(f\) that represents the problem to solve, the individual crystals are created using a straightforward formula: each value in the crystal is generated randomly within a given range.

With:

• \(v_{min}\): Minimum value that the variables of \(f\) can take.
• \(v_{max}\): Maximum value that the variables of \(f\) can take.
• \(\xi\): A random value in \(\left[0, 1\right]\)

Simply put: each value inside the crystal is randomly chosen within a predefined range, set according to the domain of the problem. Each of these crystals is a candidate solution to the problem \(f\).
Being a candidate solution means that, by replacing the elements of the crystal with the variables of the function \(f\), we get a numerical result. And what we want is to find the maximum or the minimum of \(f\), depending on the problem.

In crystallography, the bases located at the corners of the lattice — for example, like those at the vertices of the cube in Figure 1 — play a fundamental role: they are the origin of the crystal structure. By analogy, the initial crystals created (the random ones) are called main crystals and are denoted as \(C_{r_{main}}\). These main crystals are the starting point of the algorithm, which — as mentioned earlier — is structured into four update phases for the solutions. Each phase corresponds to a variant of the cubic structure:

• Simple Cubicle:

\(C_{r_{new}} = C_{r_{old}} + r C_{r_{main}}\)

• Cubicle with the Best Crystals:

\(C_{r_{new}} = C_{r_{old}} + r_{1} C_{r_{main}} + r_{2} C_{r_{b}}\)

• Cubicle with the Mean Crystals:

\(C_{r_{new}} = C_{r_{old}} + r_{1} C_{r_{main}} + r_{2} F_{c}\)

• Cubicle with the Best and Mean Crystals:

\(C_{r_{new}} = C_{r_{old}} + r_{1} C_{r_{main}} + r_{2} C_{r_{b}} + r_{3} F_{c}\)

As mentioned at the beginning, this algorithm does not use external parameters to balance exploration (finding new solutions) and exploitation (refining the good ones). The balance happens naturally, thanks to the update equations we’ve just seen.
But let’s get back on track... we’ve created four new crystals starting from the previous ones. And what do we do with them? We’ll see that in a moment. First, let me explain the sorcery behind those mysterious names:

• \(C_{r_{main}}\) : A randomly selected old crystal.
• \(C_{r_{new}}\) : The new crystal created from previous ones.
• \(C_{r_{old}}\) : The original crystal, before the update.
• \(C_{r_{b}}\) : The crystal with the best configuration, i.e., the one that gives the best value for the function \(f\).
• \(F_{c}\) : An average of the values from a crystal randomly chosen among the existing ones. \(r, r_{1}, r_{2}, r_{3}\) : Here they are, our old friends! These \(r\)’s are no longer direction vectors, but random integers. That’s what the authors of the paper decided… and who am I to argue?

The newly created crystals are used, as will be seen in the pseudocode, to replace the "old and imperfect" ones with something newer and more refined. By applying these formulas \(n\) times to the \(m\) crystals, the algorithm tries — in a probabilistic way — to find the crystal that best optimizes the problem.
We’ve now reached the end of the mathematical model.

Overview

At this point, let’s try to put everything together in pseudocode:

# Generate the first random generation of crystals
crystals = create_crystals(min_value, max_value, num_crystal)

# Compute the fitness of each crystal
crystal_fitnesses = compute_fitnesses(crystals, problem_to_solve)

# Select the best crystal based on fitness
Cr_b = get_best_crystal(crystals, crystal_fitnesses)

# Start the iterative optimization process
for _ in range(0, n_iter):
    for current_crystal in crystals:
        new_crystals = []

        # Generate random integers r, r1, r2, r3
        r, r1, r2, r3 = compute_random_r()

        # Pick a random crystal from the population
        Cr_main = take_random_crystal(crystals)

        # Pick another random crystal and compute its mean value
        Fc = compute_mean(take_random_crystal(crystals))

        # Simple cubic structure
        Cr_new = compute_simple_cubicle(Cr_old, Cr_main, r)
        new_crystals.append(Cr_new)

        # Cubic structure with the best crystal
        Cr_new = compute_cubicle_with_best(Cr_old, Cr_main, Cr_b, r1, r2)
        new_crystals.append(Cr_new)

        # Cubic structure with mean crystal
        Cr_new = compute_cubicle_with_mean(Cr_old, Cr_main, Fc, r1, r2)
        new_crystals.append(Cr_new)

        # Cubic structure with both best and mean
        Cr_new = compute_cubicle_with_best_and_mean(Cr_old, Cr_main, Cr_b, Fc, r1, r2, r3)
        new_crystals.append(Cr_new)

        # Clip values to stay within domain bounds
        new_crystals = clip_to_min_max(new_crystals, min_value, max_value)

        # Evaluate the fitness of new crystals
        new_crystal_fitnesses = compute_fitnesses(new_crystals, problem_to_solve)

        # Select the best among the new ones
        Cr_b_new = get_best_crystal(new_crystals, new_crystal_fitnesses)

        # Replace current crystal if the new one is better
        if is_new_crystal_fitness_better(Cr_b_new.fitness, current_crystal.fitness):
            substitute_current_crystal_with_new_best_one(crystals, current_crystal, Cr_b_new)

    # Update global fitness values and best crystal
    crystal_fitnesses = compute_fitnesses(crystals, problem_to_solve)
    Cr_b = get_best_crystal(crystals, crystal_fitnesses)

We have now defined all the steps of the algorithm, which allow — metaphorically speaking — the crystals to modify their internal structure (i.e., their numerical values) in order to achieve the optimal arrangement of the basis within the lattice.

I’d like to wrap up with an application example of CryStAl on a function called the Bird Function, which has the following form:

where:

\(x \in [-2\pi, 2\pi], y \in [-2\pi, 2\pi]\)

The plot of the function is quite complex (see Figure 3), and finding the minimum is anything but trivial from an analytical point of view.

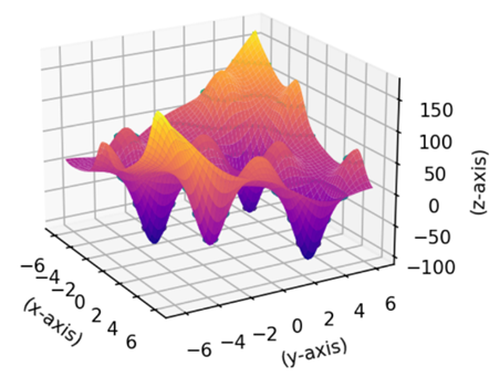Figura 3. Bird Function

Its global minimum is approximately \(f(x, y) = -106.764\) at the points:

• \(p_1 = (4.701, 3.152)\)
• \(p_2 = (−1.582, −3.130)\)

Let’s see what happens if we try to solve it using CryStAl:

# Bird Function Definition
function = lambda x: np.sin(x[0])*(np.exp(1-np.cos(x[1]))**2) + np.cos(x[1])*(np.exp(1-np.sin(x[0]))**2)+(x[0]-x[1])**2

crystal = CryStAl(function_to_optimize=function, problem_dimension=2, approach="min", 
                  lower_bound=-2 * np.pi, upper_bound=2 * np.pi, num_crystals=10, 
                  num_iterations=20)

best_fitness, Cr_b, _ = crystal.start_crystals_construction(save_history=True, verbose=False, task_name="bird_function")
print(f"Best Crystal Is {Cr_b} with fitness {best_fitness}")

The output will be something like:

Best Crystal Is [-1.58090168 -3.14616277] with fitness -106.73618458034184

Not bad, right? The result is very close to the theoretical minimum, and we get it using a parameter-free algorithm, inspired by crystallography, and — let’s be honest — also pretty stylish.

To Wrap Up

I hope this first article piqued your curiosity — and maybe even helped you discover something new! If you want to tinker with the algorithm, you can find the full source code at this link. And if you’ve fallen in love with CryStAl like I did, I also recommend checking out the paper where it all started.

Until next time.