Neurons for Dummies - 1

Se avete mai sentito parlare di reti neurali e avete pensato: "ma come diavolo fanno ad imparare?" siete approdati nel posto giusto.
Iniziamo subito con un spoiler fresco di giornata: non c'è nessuna magia, solo taaaaante moltiplicazioni, somme e derivate.
In questo articolo voglio raccontarvi con calma e senza panico, cosa succede dentro un neurone artificiale e come fa a imparare dai suoi errori, e lo faremo passo dopo passo, con un esempio pratico.

Anatomia Di Una Rete Neurale

Prima di capire come funziona una rete neurale, dobbiamo prima chiarire che cosa è una rete neurale. Iniziamo dicendo che ci sono diverse tipologie di reti neurali: convoluzionali, ricorrenti e molte altre. L'una o l'altra viene scelta in base al problema da risolvere. Quelle che prendiamo in considerazione in questo articolo sono le reti Multi Layer Perceptron (o MLP), che sono solitamente rappresentate così:

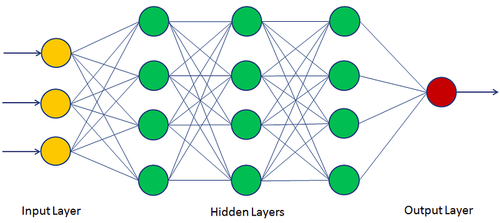Figura 1. Multi Layer Perceptron

L'immagine può sembrare semplice, ma dietro quella semplicità si nasconde un numero di concetti tale da far venir voglia di fare harakiri.
E di questa pletora di concetti... ne scalfiremo solo la superficie. Iniziamo parlando di quello che abbiamo sotto gli occhi:

• Scritte
• Frecce
• Pallini

Ogni pallina è chiamata neurone (o percettrone), e come potete vedere sono disposti in layer (o, se preferite, strati). Ogni strato è connesso al successivo in maniera completa — cioè: tutti i neuroni di un livello sono collegati a tutti i neuroni del livello successivo. Già da questo si capisce perché queste architetture prendono il nome di MLP, ovvero Multi Layer Perceptron. Ci sono tre tipi di layer:

• Layer di Ingresso: Prende i dati che forniamo in ingresso. Nell'immagine è il layer giallo.
• Layer Nascosto/i: Si chiamano così perché non interagiamo direttamente con loro. Hanno il compito di propagare in avanti i dati elaborati. Nell'immagine sono quelli verdi.
• Layer di Uscita: Contiene il risultato. Nell'immagine è il layer rosso.

Per fare un esempio pratico, supponiamo di non sapere riconoscere se in una foto ci sia un cane o un gatto (e spero vivamente che sia solo una supposizione), diamo la nostra foto al layer di ingresso che riceve i dati. Questa viene elaborata dai layer nascosti, e alla fine troviamo il risultato — cane o gatto — nel layer di uscita.
Ma prima di poter arrivare a dire "cane" o "gatto", la rete neurale ha bisogno di essere addestrata. Addestrare una rete neurale non vuol dire altro che: dargli tante foto di cani e gatti, e correggerla ogni volta che sbaglia, in modo da aggiustare il tiro per le predizioni future.
Se sei arrivato fin qui ti starai chiedendo:
"Ok ma come...?"
Calma cowboy ci arriveremo.

Dalla Rete Al Neurone

Abbiamo parlato di reti, di layer, di frecce e pallini.
Ma per capire davvero come una rete neurale prende decisioni (e come impara dai suoi errori), dobbiamo scendere di livello. Al livello del pallino.
Iniziamo partendo da quella che è la stilizzazione di un neurone biologico.

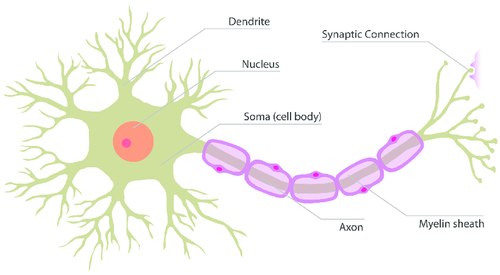Figura 2. Neurone Biologico

Nella vita ho poche convinzioni ma una di queste è che non sono un neurologo, per cui gli addetti ai lavori mi perdoneranno per la semplificazione che segue. I dendriti vengono stimolati dai segnali elettrici in ingresso. Il nucleo, insieme al soma elabora l'informazione, e l'assone la propaga verso le connessioni sinaptiche, collegandosi ai neuroni successivi.

Vi ricorda qualcosa?

Ora che sappiamo come "funziona" (il virgolettato è voluto) un neurone biologico, facciamo un grande salto di fantasia e vediamo insieme come è rappresentato un neurone artificiale, cioè l'ormai famoso pallino:

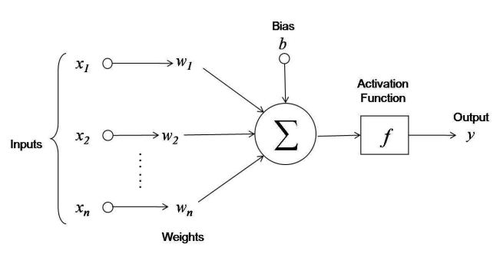Figura 3. Neurone Artificiale

Da questa immagine possiamo introdurre molti concetti dei concetti necessari al nostro scopo:

• Input: sono gli ingressi del neurone, cioè ciò che va a stimolare i dendriti.
• Pesi: Sono dei valori numerici che servono ad indicare quanto un particolare ingresso è importante. Più alto è il peso, maggiore sarà l’influenza dell'ingresso. Spoiler: i pesi sono il cuore di tutto, come vedremo a breve.
• Funzione di Trasferimento: Serve a combinare tutti gli ingressi separati in un valore unico. È l’equivalente di quello che fanno il nucleo e il soma.
• Funzione di Attivazione: Trasforma il risultato della funzione di trasferimento. L'uscita è collegata ai neuroni del layer successivo, un po’ come l’assone nei neuroni biologici.
• Bias: E' un numero puro il quale sarà visto a breve.

Mettendo tutti i singoli pezzi insieme abbiamo che: gli input \(x_i\) ed i pesi \(w_i\), passano per la funzione di trasferimento \(H\) definita come:

effettuando quella che si chiama somma pesata: ogni ingresso viene moltiplicato per il suo peso, si somma tutto, e si aggiunge il bias.
Il risultato della somma pesata viene poi passato attraverso la funzione di attivazione \(\sigma(H)\).
L'output del singolo neurone è quindi:

Ci sono moltissime funzioni di attivazione e la loro scelta dipende da diversi fattori tecnici.
Per quanto valga la pena dedicare loro un articolo a parte, per ora basti sapere che sono fondamentali per introdurre non linearità.
Che, per gli amici, vuol dire semplicemente: senza di loro, la rete non saprebbe predire correttamente nemmeno un cane da un gatto.

Confusi?

Mi stupirebbe se così non fosse. Ma tranquilli perchè ora abbiamo tutti gli ingredienti per vedere come funziona matematicamente un neurone e sarà tutto più chiaro con un esempio numerico.

Un Esempio Numerico. Il Problema AND.

Iniziamo questo nuovo paragrafo introducendo quello che è il problema da risolvere, il problema AND. L'AND tra due variabili binarie è una semplice operazione logica: il risultato è \(1\) solo se entrambe le variabili valgono \(1\) in tutti gli altri casi è \(0\). Per essere più formali, consideriamo due variabili \(A \in \{0, 1\}\) e \(B \in \{0, 1\}\) il risultato di \(AND(A, B)\) è riassunto nella seguente tabella, chiamata tabella di verità:

Qui abbiamo presentato il caso più semplice del problema AND, ma non esiste alcun vincolo sul numero di variabili.
Ad esempio, con tre variabili otterremmo la seguente tabella di verità:

Consideriamo ora una rete neurale, la più semplice possibile: composta da un solo percettrone. L'obiettivo è risolvere il problema AND a due variabili, cioè: dati gli input \(x_1\) e \(x_2\), prevedere quale sarà l'output di \(AND(x_1, x_2)\) che potrà essere \(0\) o \(1\). Poiché l'output può assumere solo due valori distinti, o sale o pepe, il problema che stiamo affrontando è un tipico problema di classificazione.

Bene: abbiamo definito il problema e l'architettura della rete neurale.
Ora ci restano da stabilire tre cose:

1. Quanti sono i nostri ingressi?
2. Quali sono i valori dei pesi e del bias?
3. Quale è la funzione di attivazione?

Rispondiamo subito:

1. Il numero di ingressi dipende dalle variabili del problema. Essendo il problema AND a due variabili, anche dette features nel contesto Machine Learning, il neurone avrà due ingressi \(x_1\) e \(x_2\), i quali valori possono essere \(0\) o \(1\).
2. In questa fase pesi e bias li assegnamo noi. Supponiamo che:
   • il peso relativo all'ingresso \(x_1\) sia \(w_1 = 0.5\),
   • il peso relativo all'ingresso \(x_2\) sia \(w_2 = 0.5\),
   • il bias sia \(b=1\).
3. Scegliamo come funzione di attivazione il gradino di Heaviside.

Il gradino di Heaviside è una semplice funzione il cui grafico è il seguente:

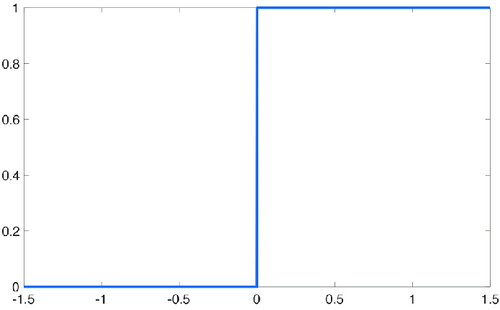Figura 4. Gradino di Heaviside

In breve, dato un qualsiasi valore \(x\) in ingresso, il gradino di Heaviside restituisce:

• \(0\) se \(x < 0\),
• \(1\) altrimenti.

Matematicamente:

Perchè proprio il gradino di Heaviside, vi starete chiedendo?
Beh come anticipato ci sono molti fattori tecnici da considerare, ma basti sapere che è quello che meglio si adatta al nostro scopo: il problema richiede una soluzione che sia \(0\) o \(1\) e il gradino di Heaviside restituisce proprio un output \(0\) o \(1\). Direi che calza a pennello no!? E invece no. Ma al momento per semplicità di esposizione ci accontentiamo, e il perchè... lo scopriremo.

A questo punto non rimane che vedere come fa una rete neurale a fare le sue predizioni. E come lo vediamo? Con una semplice sostituzione di variabili.
I casi possibili sono quattro. Ricordando che

che \(w_1 = 0.5, w_2 = 0.5, b = 1\) e che \(\sigma(H) = 1\) solo se \(H \geq 0\)

Abbiamo:

• Caso 1: \(x_1 = 0, x_2 = 0\) \(H= 0 \cdot 0.5 + 0 \cdot 0.5 + 1 = 1 \Rightarrow p = \sigma(H) = \sigma(1) = 1\)
• Caso 2: \(x_1 = 1, x_2 = 0\) \(H= 1 \cdot 0.5 + 0 \cdot 0.5 + 1 = 1.5 \Rightarrow p = \sigma(H) = \sigma(1.5) = 1\)
• Caso 3: \(x_1 = 0, x_2 = 1\) \(H= 0 \cdot 0.5 + 1 \cdot 0.5 + 1 = 1.5 \Rightarrow p = \sigma(H) = \sigma(1.5) = 1\)
• Caso 4: \(x_1 = 1, x_2 = 1\) \(H= 1 \cdot 0.5 + 1 \cdot 0.5 + 1 = 2 \Rightarrow p = \sigma(H) = \sigma(2) = 1\)

Ripetiamo quindi la tabella di verità dove riportiamo anche le predizioni del percettrone creato, dove in rosso indichiamo quelle errate e in verde quelle corrette:

Come possiamo vedere, il nostro percettrone ha fatto una sola predizione corretta su quattro. Possiamo dirlo senza mezzi termini: fa abbastanza schifo, vero?!
Ma allora perché tutto questo panegirico per arrivare a un risultato così pessimo? Semplice, perchè questa è solo la base.
Ora "rimane" da capire come migliorare i risultati, ovvero come addestriamo la rete neurale affinché smetta di fare schifo e inizi a dare predizioni sensate...
Ma intanto un risultato importante l'avete già portato a casa:
Ora sapete che la "magia" dietro le predizioni, o almeno una bella fetta di essa, non è poi così magica.

Conclusioni

Lasciate che mi congedi con questo breve snippet di codice, che non fa altro che replicare esattamente quello che abbiamo visto insieme.

# Definizione del gradino di Heaviside
class Heaviside(Activation):

    def __call__(self, x) -> int:
        result = 1
        if x < 0:
            result = 0
        return result

# Definizione del percettrone
class Perceptron:

    def __init__(self, dimension: int, activation: Activation = None):
        self._weights = np.zeros(dimension)
        self._bias = 0.
        self._activation = activation

    def __call__(self, inputs: np.ndarray) -> float:
        weighted_sum = np.dot(inputs, self._weights) + self._bias
        result = weighted_sum
        if self._activation is not None:
            result = self._activation(weighted_sum)
        return result

# Run del codice 
perceptron = Perceptron(dimension=2, activation=Heaviside())
perceptron.weights = np.array([0.5, 0.5])
perceptron.bias = 1.

cases = [[0, 0], [0, 1], [1, 0], [1, 1]]
true = [0, 0, 0, 1]
for i, (case, y) in enumerate(zip(cases, true)):
    prediction = perceptron(inputs=np.array(case))
    print(f"Case {i + 1}. Input = {case}, True Result = {y}, Predicted Result = {prediction}")

L'output dovrebbe essere il seguente:

Case 1. Input = [0, 0], True Result = 0, Predicted Result = 1
Case 2. Input = [0, 1], True Result = 0, Predicted Result = 1
Case 3. Input = [1, 0], True Result = 0, Predicted Result = 1
Case 4. Input = [1, 1], True Result = 1, Predicted Result = 1

Se siete curiosi, vi invito a vedere l'intero codice qui.

E per concludere... pensavate che mi fossi dimenticato, vero?! Che vi avessi venduto fuffa. E invece no cari miei, vi invito a leggere la seconda parte. Non vorrete mica fermarvi a come la rete predice, vero?! Non si può vivere senza sapere come impara. Si lo so, sono peggio delle uscite della De Agostini... ma tant'è. In attesa della seconda parte vi saluto.

Alla Prossima.