Ed eccoci qui, con la terza parte dell'articolo dedicato al neurone. Inizialmente ne avevo preventivate due ma che volete che vi dica, mi sono lasciato prendere la mano. Non potevo mica lasciarvi senza spiegare perché le reti sono composte da tanti neuroni o come si arriva alla formulazione dell'aggiornamento dei pesi. Non me lo sarei mai perdonato. In ogni caso, nella prima parte ho spiegato come un neurone predice, nella seconda parte ho spiegato come avviene l'apprendimento. Questa terza parte invece è dedicata ad alcuni aspetti che avevo lasciato fuori, ma che possono tornare utili. Come si suol dire tutto fa brodo no!?
La Regola Della Catena
La regola della catena è una regola di derivazione per funzioni composte, cioè funzioni che incapsulano altre funzioni al loro interno. In parole povere:
La derivata di una funzione composta si ottiene derivando la funzione esterna e moltiplicando per la derivata della funzione interna.
Tradotto in formule, se abbiamo due funzioni: \(v = h(z), u = g(v), y = f(u) \Rightarrow y = f(g(h(z)))\) derivando si ha:
Una rappresentazione alternativa è la seguente:
Ad esempio, dati:
La funzione è:
e la sua derivata:
La Discesa Del Gradiente
In questa sezione vediamo come si arriva alla formulazione della discesa del gradiente. Non vuole essere un trattato di matematica, ma solo fornire un’idea generale del perché funziona, quindi ometterò molti dettagli tecnici per non
appesantire la trattazione.
I puristi della matematica tra voi mi perdoneranno.
Prima di tutto introduciamo la Serie di Taylor. Questa permette di approssimare una funzione \(f(x)\)
in un punto vicino uno noto \(x_0\), utilizzando le derivate di \(f\) calcolate in quel punto. E non è proprio quello che facciamo con la funzione di errore?!
Valutiamo la funzione nei dintorni di dove ci troviamo, per scegliere dove andare.
Ma torniamo a noi. Matematicamente si scrive così:
Facciamo un esempio numerico e consideriamo:
Le derivate sono:
e quindi con le dovute sostituzioni scriviamo:
Compariamo i grafici di:
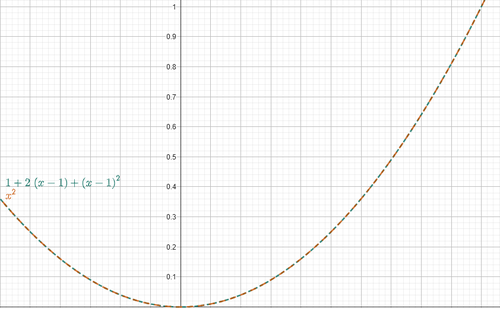Figura 1. Approssimazione di Taylor
Come si può vedere, le due funzioni hanno lo stesso andamento nell’intorno di \(x_0=1\), quindi \(g(x)\) approssima correttamente \(f(x)\) in quel punto.
Nella serie di Taylor, più termini (cioè più derivate) consideriamo, migliore sarà l’approssimazione della funzione. Ma per i nostri scopi, ci accontentiamo di fermarci alla prima derivata.
Questa formula ci dice come si comporta localmente la funzione \(f(x)\). La derivata prima, \(f'(x_0)\) ci indica la velocità e la direzione con cui la funzione cresce, mentre \((x-x_0)\) rappresenta uno spostamento rispetto al punto di partenza. Ma ricordiamoci il nostro obiettivo: minimizzare. Non vogliamo andare nella direzione di crescita, ma in quella opposta, e vogliamo farlo con un passo piccolo, scelto a piacere. Per questo, possiamo scrivere lo spostamento come:
dove:
- \(\eta\) è l’ampiezza del passo
- \(-f'(x_0)\) è la direzione opposta alla crescita
Quindi possiamo scrivere:
Vi ricorda qualcosa?
Ma torniamo a noi. Sostituendo questo nella formula di Taylor, otteniamo:
Per semplicità di notazione scriviamo:
e
dove:
- \(x_t\) è il punto di partenza
- \(x_{t+1}\) è il punto di arrivo
Per cui:
A questo punto supponiamo che \(f\) sia una Funzione Convessa e Lipschitziana, possiamo affermare la seguente disuguaglianza:
con
dove \(L\) è una costante Lipschitz.
A parole: la funzione \(f\), passando dal punto \(x_t\) al punto \(x_{t+1}\), diminuisce, a patto di scegliere
il valore \(\eta\) sufficientemente piccolo. Ed è proprio quello che volevamo!
Con la legge
la funzione si riduce a ogni passo.
Quindi, se poniamo \(f\) come la funzione di errore e \(x\) come un generico peso, abbiamo appena dimostrato la formula della discesa del gradiente.
Questa dissertazione è solo per fornire una "semplice" intuizione. Se cercate una dimostrazione formale e rigorosa, vi consiglio di dare un’occhiata qui.
Sulle Funzioni Di Attivazione
In questa sezione rispondiamo finalmente al perché il Gradino di Heaviside è stato spietatamente scartato come funzione di attivazione. Se avete letto tutto l'articolo avete anche visto che la backpropagation richiede questo calcolo:
dove:
- \(\frac{\partial p }{\partial net}\) è la derivata della funzione di attivazione rispetto l'output della funzione di trasferimento.
- \(\frac{\partial L }{\partial p}\) è la derivata dell'errore rispetto la predizione.
Per poter calcolare queste derivate, sia la funzione di errore \(L\), sia la funzione di attivazione \(\sigma\) devono essere derivabili. Il problema è che il gradino di Heaviside ha una discontinuità in \(x=0\), per cui non è derivabile e questo è un problema. O meglio, per essere onesti, non è derivabile nel senso classico ma lo è nella teoria delle distribuzioni. Difatti la sua derivata è la Delta di Dirac. Ma senza perderci in troppe astrazioni, diciamo che non è una derivata che possiamo usare direttamente nel nostro algoritmo. Infatti anche la funzione di attivazione ReLU non è derivabile in \(x=0\), ma nessuno la scarta per questo. Nell'immagine seguente potete vedere il suo andamento:
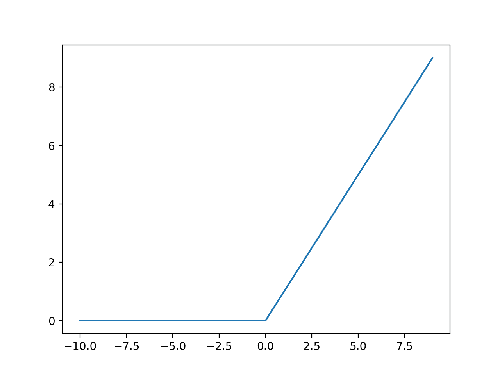Figura 2. ReLU
Quindi, perché tutta questa avversione verso Heaviside?
Presto detto: sebbene ReLU non sia derivabile in \(x=0\), non è discontinua in quel punto. Possiamo quindi assegnare artificialmente un valore di derivata tra 0 e 1: la funzione è subderivabile. Con Heaviside, invece, questo non è possibile. E anche se (per assurdo) decidessimo di usare la Delta di Dirac come derivata... guardate qui:
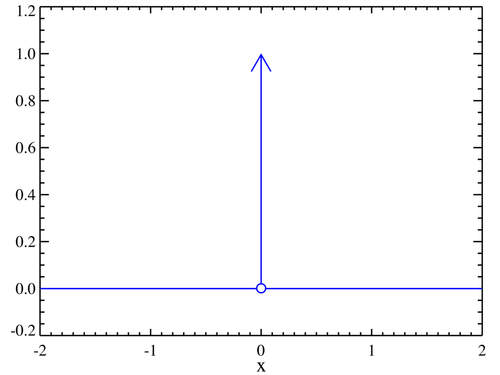Figura 3. Delta di Dirac
Come potete vedere, è nulla ovunque, tranne che in \(x=0\). Questo significa che il gradiente sarebbe sempre nullo, che i pesi non cambierebbero mai e la rete neurale non imparerebbe nulla.
C'è infine un'ultima, seppur secondaria, criticità: la Binary Cross Entropy divergerebbe ad infinito se la predizione fosse esattamente \(0\) o \(1\). Questo non succede con la sigmoide perchè
assume quei valori solo asintoticamente.
Da Uno A Molti
Quest'ultima sezione vuol fornire un'idea generale del perché nasce l'esigenza di usare reti con molti neuroni. In fondo, abbiamo visto che un singolo percettrone
è effettivamente in grado di arrivare a una soluzione, no!? Avete visto coi vostri occhi: continuando l'addestramento, i pesi vengono i pesi si modificano fino a risolvere correttamente il problema AND.
Quindi... perché aggiungere complessità?
Iniziamo il ragionamento guardando alla funzione di trasferimento. Per il problema AND in due dimensioni abbiamo:
Ad alcuni di voi questa formula non dirà nulla. Ad altri farà riaffiorare brutti ricordi legati all'equazione della retta, in forma implicita. Quindi di fatto quello che sta facendo la backpropagation è trovare i coefficienti della retta per permettere questo:
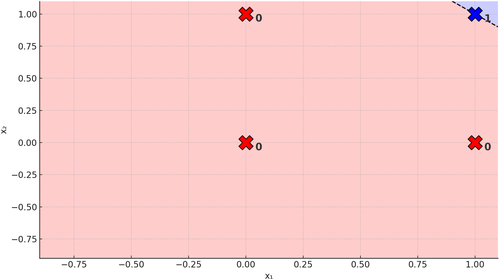Figura 4. Retta su Problema AND
Cioè separare i casi in cui la soluzione è \(0\) da quelli in cui è \(1\). Riuscire a fare questo significa che possiamo separare linearmente le soluzioni del problema e abbiamo visto
che un singolo percettrone è perfettamente in grado di farlo.
Consideriamo un altro problema ora, chiamato problema XOR. E' un'operazione logica come il problema AND, ma ha una tabella di verità diversa:
Vediamo geometricamente cosa succede:
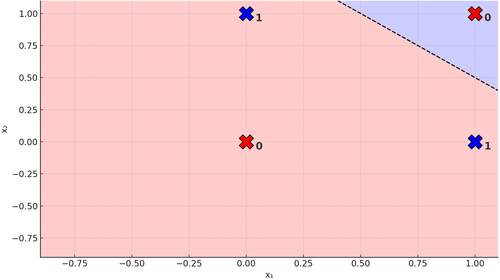Figura 5. Retta su Problema XOR
Sbattete pure la testa, imprecate quanto volete, ma non riuscirete mai a trovare una retta che separi gli \(0\) dagli \(1\). E' impossibile. Ed è proprio per questo che il problema XOR si dice non linearmente separabile. Ahimè potessimo aggiungere un'altra retta, allora sì che potremmo fare questo:
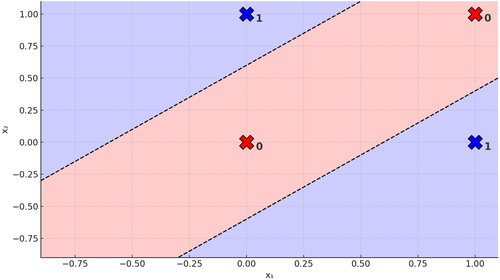Figura 6. Due rette su Problema XOR
Ma un momento... chi ci dice che non possiamo!? Dopotutto, un neurone crea una retta quindi... due neuroni creano due rette, no? Ed ecco qui che abbiamo giustificato il perché abbiamo bisogno di più neuroni. Ma questo quanto cambio tutto quello visto finora!? Prima di rispondere, guardiamo come diventa la nostra rete neurale:
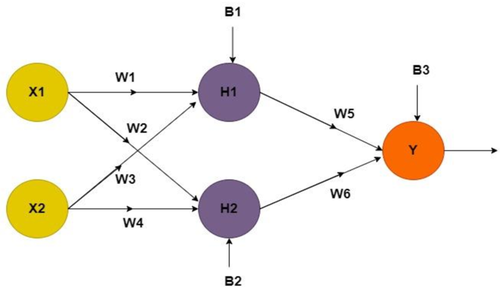Figura 7. Rete Neurale per Problema XOR
Se vi state chiedendo: "ma come Luca, hai detto che bastava l'aggiunta di un solo neurone! Sono indignato!1!! La risposta è si, confermo che è vero.
Ma le reti feed-forward classiche pretendono che il numero di neuroni in ingresso sia pari al numero di features quindi ve lo tenete così. Magari in futuro vi racconterò
la bellissima storia della neuroevoluzione dove le cose cambiano parecchio. Ma torniamo a noi...
Le cose in realtà rimangono le stesse, l'unica differenza è che dobbiamo scendere in profondità nell'equazione della derivata dell'errore rispetto al peso, perchè ora l'uscita
di un neurone diventa l'ingresso del successivo. Concentrandoci sui neuroni \(Y\) e \(H_1\), l'output di \(H_1\) è:
quello di \(Y\) è:
Riscrivendo in una forma che abbiamo già visto abbiamo che:
dove:
- \(\frac{\partial net_Y}{\partial h_1}\) è la derivata della funzione di trasferimento di \(Y\) rispetto la funzione di attivazione di \(H_1\)
- \(\frac{\partial h_1}{\partial net_{H_1}}\) è la derivata della funzione di attivazione di \(H_1\) rispetto la sua funzione di trasferimento
- \(\frac{\partial net_{H_1}}{\partial w_1}\) è la derivata della funzione di trasferimento di \(H_1\) rispetto il peso \(w_1\)
E direi, per la nostra sanità mentale, che possiamo fermarci qui ma lo stesso identico ragionamento vale per:
E con \(n\) neuroni? E' come avere \(n\) rette (o spezzate) che, tutte insieme, formano una curva che è in grado di separare i dati non linearmente separabili. Insomma... è tranquillamente in grado di fare questa mostruosità
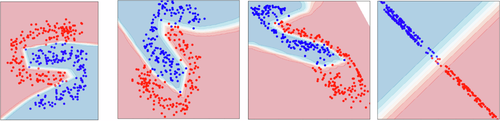Figura 8. Confine Decisionale della Rete con Tanti Neuroni
Ultima nota prima di passare alle conclusioni. Per semplicità, abbiamo considerato il caso bidimensionale e quindi abbiamo parlato di rette, ma il discorso resta valido anche per spazi a più dimensioni. In quel caso non parliamo di rette ma di iperpiani.
Conclusioni
Bene ragazzi, eccoci arrivati alla fine della serie di articoli relativi al neurone. Per fare una grande citazione:
Qui infine si scioglie la nostra compagnia... non vi dirò non piangete, perché non tutte le lacrime sono un male.
Ovviamente intendo la compagnia del neurone eh, perché altri articoli vi aspettano. Nella vita ci sono poche cose certe: morte, tasse e un altro mio articolo. Spero che questa serie vi sia piaciuta almeno quanto è piaciuto a me scriverla.
Alla Prossima.