Sono da poco passate le feste. E sì, lo so che siamo a febbraio, ma la stesura di questo articolo è iniziata il 5 di gennaio quindi niente, sono da poco passate le feste. Tutti noi abbiamo fatti pranzi, cene e cenette e sono sicuro che siete stati ammorbati dai soliti discorsi qualunquistici di politica fatti dal parente operaio (ma medico nel tempo libero) che sà che il vaccino fa venire l'autismo. Perché lui si è informato. Già me lo immagino, già sento echeggiare dentro di me
Chernobyl ha fatto anche cose buone...
Ah no un momento, non era proprio così la frase. Vabbè allora riniziamo, questa volta meno parafrasato... cosa ci ha lasciato Chernobyl!? E prima che me lo chiedete, intendo oltre all'ignoranza dilagante ed alla paura ancestrale dell'energia nucleare (se non si fosse capito sono un sostenitore dell'energia atomica). Ebbene sì, ci ha lasciato un bellissimo algoritmo di ottimizzazione. E dato che sono un grande fan di tutto ciò che è strano, ho deciso di parlarne. Quindi prendete tutti i giubbotti di piombo e iniziamo.
3, 2, 1... Ignition
Ignition vuol dire accensione, ma ad accendersi non è un motore, bensì un reattore. Ora, non dico che dobbiamo ringraziare Djatlov per il suo pessimo lavoro, ma grazie al suo pessimo lavoro è scappato fuori questo algoritmo. Certo sto proprio vedendo il bicchiere mezzo pieno ma siamo in ballo, balliamo.
Iniziamo dicendo che è un algoritmo physics-inspired, e da buon algoritmo metaeuristico, ha come obiettivo la ricerca dell'ottimo e in cosa consiste ci arriveremo. Ora lungi da me spiegare la fisica delle particelle, anche perché non la so e sinceramente studiarla per scrivere un articolo su un algoritmo metaeuristico mi sembra un pò overkill. In ogni caso quando esplode una centrale nucleare, tra i vari isotopi e particelle emesse dal nucleo instabile, ci sono i tre protagonisti della nostra storia che sono particelle alfa, particelle beta e raggi gamma.
- Le particelle Alfa sono quelle dalle ossa grosse, e quindi piú "lente". Pensante che arrivano a solo \(\sim 5 \%\) della velocità della luce, povere sfigate! In ogni caso sono composte da due protoni e due neutroni. Hanno quindi una carica positiva che nella materia è molto alta, e proprio per questo sono fortemente ionizzanti (per inciso, ionizzante \(\rightarrow\) distruzione molecolare \(\rightarrow\) avvelenamento da radiazioni \(\rightarrow\) ti sciogli \(\rightarrow\) muori). Il fatto che sono molto ingombranti peró, le rende anche poco penetranti. A capirci se state dietro un foglio di carta state al sicuro, almeno fino a quando non le respirate e/o ingerite, in tal caso è stato bello e ci vedremo dall'altra parte dello Stige.
- Le particelle Beta hanno seguito la chetogenica e sono un “pochino” più snelle: arrivano a circa il \(\sim 30–90 \%\) della velocità della luce. La loro massa è ridotta, essendo composte da un elettrone, ed hanno carica negativa. Sono un pó più insidiose delle alfa, soprattutto dall’esterno, ma si schermano tranquillamente con pochi millimetri di metallo come l’alluminio. Se non siete dietro una schermatura, però, cavoli vostri. Sono meno ionizzanti delle alfa, ma essendo spesso molto energetiche, l’interazione con gli atomi del nostro corpo fa schizzare via gli elettroni orbitanti (ed ecco che torna la distruzione molecolare).
- I raggi Gamma sono onde elettromagnetiche. Sono costituiti da fotoni (sai, i responsabili della trasmissione della luce) e quindi non hanno massa.
In pratica sono l'Ariana Grande delle particelle e viaggiano alla velocità della luce. A meno che non hai alzato una parete di
piombo in stile Fortnite, hanno un potere penetrante molto elevato. La loro pericolosità deriva da come interagiscono con la materia. Possono farlo in tre modi:
- Effetto Fotoelettrico: Tutta l'energia del fotone è trasmessa ad un elettrone dell'atomo il quale viene espulso dalla sua orbita.
- Effetto Compton: Il fotone cede parte della sua energia con il risultato di ottenere un elettrone libero e molto incazzato.
- Effetto Coppia: Parte dell'energia viene convertita in massa creando un elettrone e un positrone che interagiscono con gli altri elettroni come nelle particelle beta.
Cosa succede se si viene colpiti dai raggi gamma?! Se ti va bene diventi l'incredibile Hulk, se ti va male (e ti andrà male), ricadi nelle casistiche precedenti e ciaone.
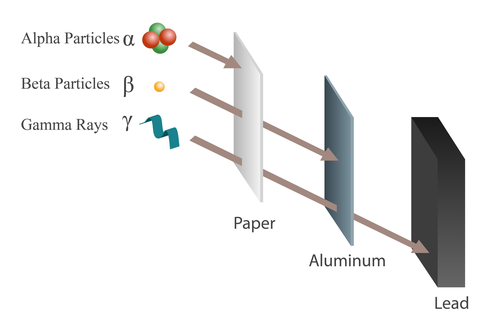 Figura 1. Particelle Alfa e Beta, raggi Gamma
Figura 1. Particelle Alfa e Beta, raggi Gamma
Concludiamo questo paragrafo con una domanda (e anche una risposta). Se dovesse malauguratamente esplodere una centrale, qual é la prima cosa che fanno le persone? Esatto, scappano. Cercano di mettersi in sicurezza per sfuggire a tutte le brutte cose presentate. In fondo chi é che vuol diventare un energumeno verde e incazzato?
Radiazioni, Panico e Minimi Locali
Ci siamo fermati, nel precedente paragrafo, con persone che scappavano urlando. Ora non voglio dire che le radiazioni ionizzanti come dei segugi, vadano in cerca delle persone, ma in questo algoritmo le persone rappresentano proprio l'obiettivo. Una persona corre via dal punto di esplosione, e le nostre amiche vanno alla sua ricerca che corrisponde con la ricerca dell'ottimo. Macabro? Sì. Poco realistico? Anche. Ma dai, è fighissimo (magari per i cittadini di Pripyat lo è un pó meno). Questo vuol dire ricercare l'ottimo nel Chernobyl Disaster Optimizer (CDO)! Sul come invece, beh... continuate la lettura.
Abbiamo individuato i quattro elementi necessari al CDO. Vediamo come sono utilizzati algoritmicamente.
L'Uomo
L'uomo, la nostra vittima sacrificale. Il futuro Hulk dei poveri. Come abbiamo detto lui scappa, ed intuitivamente piú si allontana piú si sente al sicuro, fino a fermarsi. Questo viene modellato tramite la seguente formula:
Formula 1. Decadimento Della Velocità
Cioè la velocità di fuga è inizialmente massima, \(3mph\) (si, l'autore usa le miglia orarie come unità), e man mano che l'algoritmo iterativo procede, la velocità diminuisce fino ad azzerarsi. Nella formula:
- \(it\) è l'iterazione corrente
- \(n_{it}\) è il numero di iterazioni che saranno svolte dall'algoritmo.
Come si vedrà dalle formule successive, Le particelle non vedono l’uomo e non sanno dove si trovi, ma vengono premiate quando gli si avvicinano. Chi si avvicina di più diventa guida per le altre.
Particelle e Raggi
Le nostre ambasciatrici che portano pena: le particelle dell'algoritmo. Queste partono dal punto dell'esplosione in cerca dell'uomo da irradiare. Come moltissimi algoritmi metaeuristici, CDO è population based. Questo vuol dire che abbiamo una famiglia di particelle dove ogni particella è una lista di dimensione pari alla dimensionalità del problema da risolvere, e rappresenta una possibile soluzione al problema stesso. Ad ognuna di esse è associata una fitness che serve a stabilire quanto una particella è brava a risolvere un problema. Piú la fitness è alta/bassa (in funzione del tipo di problema, se massimo o di minimo), più si avvicina alla soluzione ottimale nello spazio di ricerca. Andiamo a vedere come, matematicamente, si spostano per trovare il loro bersaglio. Nella mia implementazione, tutte le particelle hanno posizioni casuali, e le migliori (o leader) vengono inizialmente poste nell’origine, che nella metafora coincide con il punto dell’esplosione.
def _update_best_particles(self, fitness: float, pos: np.ndarray, alpha_score: float, alpha_pos: np.ndarray,
beta_score: float, beta_pos: np.ndarray, gamma_score: float, gamma_pos: np.ndarray):
is_alpha_better = self._is_better(fitness, alpha_score)
is_beta_better = self._is_better(fitness, beta_score)
is_gamma_better = self._is_better(fitness, gamma_score)
if is_alpha_better is True:
alpha_score, alpha_pos = fitness, pos.copy()
if is_alpha_better is False and is_beta_better is True:
beta_score, beta_pos = fitness, pos.copy()
if is_alpha_better is False and is_beta_better is False and is_gamma_better is True:
gamma_score, gamma_pos = fitness, pos.copy()
return alpha_score, alpha_pos, beta_score, beta_pos, gamma_score, gamma_pos
def optimize(self):
alpha_pos = np.zeros(self._dim)
beta_pos = np.zeros(self._dim)
gamma_pos = np.zeros(self._dim)
alpha_score = np.inf if self._approach == "min" else -np.inf
beta_score = np.inf if self._approach == "min" else -np.inf
gamma_score = np.inf if self._approach == "min" else -np.inf
...
for it in range(self._n_iter):
for particle_i in range(self._n_particles):
current_particle = self._clip(particles[particle_i])
particles[particle_i] = current_particle
fitness = float(self._function_to_optimize(current_particle))
(alpha_score, alpha_pos, beta_score,
beta_pos, gamma_score, gamma_pos) = \
self._update_best_particles(fitness, current_particle, alpha_score, alpha_pos,
beta_score, beta_pos, gamma_score, gamma_pos)
...
Snippet 1. Definizione Dei Leader
Come si vede dallo Snippet 1 vengono ricavate solo le tre leader alfa, beta e gamma, ovvero le migliori soluzioni trovate fino a quel momento.
Questo perché le migliori sono quelle piú vicine alla soluzione ottimale (all'uomo), e sono buone candidate per guidare
l'esplorazione dello spazio di ricerca delle altre, in una data iterazione. Inoltre l'aggiornamento delle particelle avviene con criteri stringenti come si può notare
dalla funzione _update_best_particles. Questo permette di non avere cambiamenti continui e quindi di avere una evoluzione controllata
delle posizioni delle particelle, favorendo la convergenza della soluzione.
Fin qui abbastanza chiaro, no? Particelle a caso, fitness, migliori che emergono. Ora arriva la parte interessante: come diavolo le facciamo muovere?
Iniziano ora un pò di formulette. Per ogni particella \(\xi\), o meglio per ogni componente \(col\) di ogni particella \(\xi\), calcoliamo quello che l'autore chiama Gradient Descent Factor. Non lasciatevi però ingannare dal nome, non si tratta di un gradiente poiché non compare alcuna derivata. È invece un coefficiente che indica quanto fortemente una componente viene spinta verso una delle particelle leader (alpha, beta o gamma), che in quel momento rappresentano le migliori soluzioni trovate. In formule abbiamo:
Formula 2. Gradiente Di Discesa
Si ok sono tante scritte. Ma andiamo per ordine. Prima di tutto inizio dicendo che la \(p\) al pedice, serve a indicare il leader di riferimento, quindi \(p=\alpha, \, \beta, \, \gamma\). Questo perché le formule cambiano a seconda del leader considerato, a partire dalla grandezza \(\varphi_{p}\) che puó essere interpretata come un fattore di scala:
Formula 3. Fattori Di Scala
Per quanto riguarda il termine \(POS_{p}^{col}\), rappresenta semplicemente la componente posizione della particella leader. Infatti abbiamo detto che ogni particella è una lista, e quel \(col\) serve ad indicare l'i-esimo elemento della lista. A scanso di equivoci, se considerassimo un problema di ottimizzazione bidimensionale, la Formula 2 verrebbe eseguita sei volte per ogni particella. Questo perché viene eseguita una volta per ogni elemento della lista, e per ogni elemento si considera prima il leader \(\alpha\), poi il \(\beta\) ed infine il \(\gamma\).
Passiamo al termine successivo, \(PROP_{p}\). Possiamo vederla come un'area di influenza: più questa area è ampia, più particelle ricadono sotto l’effetto del leader e quindi tendono a seguirlo, ossia il loro spostamento viene calcolato rispetto a questa regione. E' definito cosí:
Formula 4. Fattori Di Propagazione
In questa formula vediamo vecchi e nuovi amici. Abbiamo già introdotto \(\varphi_{p}\) e \(WS\). Non c'è bisogno di dirvi cosa è \(\pi\). Invece \(r_{1, \, p}^2\), è un valore numerico casuale compreso tra \(0\) e \(1\) (il pedice \(p\) serve a indicare che ogni leader avrà un proprio raggio casuale), \(rand_p \left( 0, \, 1 \right)\) è stessa identica cosa. Molto piú interessante invece è \(\upsilon_{p}\). Questa rappresenta una velocità associata al leader ed è in funzione del leader considerato. E' definita cosí:
Formula 5. Velocità Dei Leader
Se ricordate, nei paragrafi precedenti avevo parlato di quanto fossero veloci le particelle. Ebbene quel discorso è stato necessario proprio per arrivare a questo momento. Ogni leader ha una sua velocità definita come il logaritmo in base \(10\) di un numero casuale preso tra \(1\) e la velocità massima per quel tipo di particella. L’uso del logaritmo serve a ridurre valori potenzialmente molto grandi, evitando l'instabilità dell'algoritmo.
Ci siamo quasi, manca l'ultimo ingrediente. \(D_{p}\) rappresenta la distanza tra la particella corrente \(\xi\) e l’effetto del leader \(p\), tenendo conto della sua propagazione. E' definita cosí:
Formula 6. Distanza
In questa formula abbiamo: \(A_{p}\) che è l'area di propagazione associata al leader \(p\) ed è una misura dell'estensione del suo spazio di ricerca. Analogamente a prima, si calcola in questo modo:
Formula 7. Area Di Propagazione
E \(\xi_i^{col}\) e \(POS_{p}^{col}\) che sono già stati introdotti. Dato che repetita iuvant, \(\xi_i^{col}\) è il valore contenuto nella posizione \(col\) della particella \(i-esima\) (da non confondere con la leader), e \(POS_{p}^{col}\) è il valore contenuto nella posizione \(col\) della particella leader \(p\).
Ok scherzavo, non era proprio l'ultimo ingrediente. Ma ora che abbiamo definito tutte le formule necessarie possiamo calcolare \(GDF_{p}\) e quindi procedere con il calcolo del nuovo valore delle componenti posizione di ogni particella. Per cui aggiorniamo il valore di \(\xi_i^{col}\) nel seguente modo:
Formula 8. Aggiornamento Componente Posizione
Si, sono tantissime formule ma giuro che sono finite. Per cui ecco uno snippet di codice che implementa quanto scritto:
def optimize(self):
...
new_positions = np.empty_like(particles)
for particle_i in range(self._n_particles):
for particle_col in range(self._dim):
particle_col_val = particles[particle_i, particle_col]
r1 = self._np.random()
r2 = self._np.random()
alpha_prop = (np.pi * r1 * r1) / (0.25 * speed_alpha) - walking_speed * self._np.random()
alpha_prop_area = (r2 * r2) * np.pi
alpha_col_val = alpha_pos[particle_col]
D_alpha = abs(alpha_prop_area * alpha_col_val - particle_col_val)
gdf_alpha = 0.25 * (alpha_col_val - alpha_prop * D_alpha)
r1 = self._np.random()
r2 = self._np.random()
beta_prop = (np.pi * r1 * r1) / (0.5 * speed_beta) - walking_speed * self._np.random()
beta_prop_area = (r2 * r2) * np.pi
beta_col_val = beta_pos[particle_col]
D_beta = abs(beta_prop_area * beta_col_val - particle_col_val)
gdf_beta = 0.5 * (beta_col_val - beta_prop * D_beta)
r1 = self._np.random()
r2 = self._np.random()
gamma_prop = (np.pi * r1 * r1) / speed_gamma - walking_speed * self._np.random()
gamma_prop_area = (r2 * r2) * np.pi
gamma_col_val = gamma_pos[particle_col]
D_gamma = abs(gamma_prop_area * gamma_col_val - particle_col_val)
gdf_gamma = gamma_col_val - gamma_prop * D_gamma
new_positions[particle_i, particle_col] = (gdf_alpha + gdf_beta + gdf_gamma) / 3.0
...
Snippet 2. Aggiornamento Delle Particelle
Vorrei concludere questo paragrafo con una nota. Qualsiasi buon algoritmo metaeuristico affronta il problema dell'exploration vs exploitation, cioè continuare la ricerca a livello globale ma allo stesso tempo continuare a sfruttare le soluzioni buone trovate fino a quel momento. In questo algoritmo questo è fatto tramite i leader e le loro aree di propagazione. Infatti se ben ricordate, il leader alfa non va molto lontano essendo schermato facilmente ed avendo velocità ridotta. Questo è quello che avviene anche nell'algoritmo. Il leader alfa incentiva una ricerca locale e quindi lo sfruttamento delle soluzioni buone già note. Tramite la sua area di propagazione si cerca in un suo intorno locale. A scalare invece, beta e gamma, che grazie a velocità e propagazioni maggiori esplorano regioni più lontane dello spazio di ricerca, fino ad allora sconosciute.
Al termine dell'algoritmo, la soluzione migliore (che vi ricordo essere la particella con fitness piú alta/bassa) è data dal leader alfa.
L'Esplosione
Come si innesca questo algoritmo?! Beh semplicemente istanziando e richiamando la classe da me definita:
function = lambda x: np.sin(x[0]) * (np.exp(1-np.cos(x[1])) ** 2) + np.cos(x[1]) * (np.exp(1-np.sin(x[0])) ** 2) + (x[0]-x[1]) ** 2
cdo = CDO(n_particles=30, dim=2,
approach='min', n_iter=20,
bounds=(-2 * np.pi, 2 * np.pi), function_to_optimize=function)
best_fitness, best_particle, _ = cdo.optimize()
print(f'Best Fitness is {best_fitness} with Particle {best_particle}')
Snippet 3. Utilizzo Dell'Algoritmo
Vale la pena sprecare due parole sugli argomenti del costruttore.
n_particlesindica il numero di particelle che volete nella vostra popolazione di particelle. Tendenzialmente piú è alto, maggiore è la probabilità di raggiungere l'ottimo, ma comporta un rallentamento dell'algoritmo.function_to_optimizeedimsono la funzione matematica da ottimizzare, e la sua dimensionalità. Nel mio caso specifico ho usato come funzione la Bird Function che ha dimensione \(2\) ed è nota per la sua difficoltà nel calcolo del minimo.approachindica se si vuole minimizzare (min) o massimizzare (max).boundsindica i limiti di esistenza della funzione. E' utile quando sappiamo di dover cercare l'ottimo in una determinata porzione del dominio.
Lanciando questo snippet dovreste ricevere un output simile:
Best Fitness is -106.3248972989146 with Particle [4.74192243 3.21810325]
dove i valori contenuti all'interno della particella sono le coordinate \((x, \, y)\) che portano vicinissimi al minimo della funzione, nel dominio fornito. Degno di specifica è l'utilizzo della parola 'dovreste', dato che è un processo probabilistico.
Conclusioni
Questi algoritmi esotici devo dire che mi piacciono molto ed è stato divertente studiarlo e implementarlo. Ma questo con il senno di poi. Il paper originale infatti, non solo è scritto piuttosto male ma contiene anche diverse imprecisioni nelle formule. Per questo motivo, nella stesura di questo articolo mi sono basato in parte su quello, in parte su un secondo paper piú recente e sul codice Matlab fornito dall'autore dell'algoritmo. Ne è venuto fuori, di fatto, un lavoro di ingegneria inversa e ricostruzione delle informazioni, necessario per dare una forma coerente e utilizzabile all’algoritmo. Come sempre, vi lascio il link alla mia implementazione per poter dare un’occhiata al codice e fare i vostri esperimenti. Occhio alle radiazioni.
Alla Prossima.

