C'era una volta una rete neurale che non voleva funzionare layer su layer come tutte le sue amiche. No, lei voleva essere continua, fluida, dinamica. Voleva essere una equazione differenziale. Questo non è il classico incubo dei matematici. Non c'è Freddy Krueger che li sveglia nel cuore della notte sussurrando risolvi il Demidovich, né derivate che appaiono sui muri col sangue. È, al contrario, un modo elegante e concettualmente affascinante per ripensare l’architettura delle reti neurali: sto parlando delle Neural ODE.
In questo articolo, o meglio serie di articoli, vediamo cosa succede quando il mondo del Deep Learning incontra quello delle
equazioni differenziali ordinarie (ODE). Spoiler: nessuno si fa male (forse), ma qualcuno potrebbe uscirne un po' più confuso del solito.
E se vi state chiedendo:
Ma che bisogno c'è?
tranquilli: come sempre la risposta è a metà tra perché posso
e perché è concettualmente fighissimo. Ma non solo. Le Neural ODE offrono un'alternativa elegante
per modellare dinamiche temporali complesse. Sono particolarmente utili quando servono
continuità nel tempo, memoria contenuta e strutture flessibili.
Ovviamente non tutto è oro, ma questo lo vedremo.
Iniziamo partendo da una galassia lontana lontana...
In Principio Era Derivato
Mi rifiuto di credere che voi, avventori di questo umile articolo, vi ricordiate davvero cosa siano le ODE. Diciamocelo: da quando ci siamo laureati, chi ne ha più risolta una? E se lo avete fatto... mi spiace per voi. In ogni caso, per comprendere a fondo le Neural ODE dobbiamo partire da mooolto lontano: dal concetto di derivata.
Quando parliamo di derivata, parliamo di cambiamento. In particolare rispondiamo alla domanda:
Quanto cambia il valore di \(f(x)\) quando cambio leggermente il valore \(x\)?
Traduciamo questa frase nella lingua della matematica. Stiamo cambiando il valore di \(x\), e lo cambiamo aggiungendo un valore molto piccolo: \(h\). Quello che vogliamo misurare però è il cambiamento, e quindi scriviamo:
Abbiamo il nostro cambiamento, ma cambiamento rispetto a cosa!? La formula così scritta non ci fornisce questa risposta.
È come dire: ho avuto un aumento 1000 €.
Buon per te, ma 1000 € in quanto tempo? Se è 1000 € in un anno non è questo gran risultato,
se è 1000 € in un'ora vengo a lavorare con te.
E' bastata una singola parola in più che è cambiato tutto. Questo perché la singola parola, ci ha dato la rapidità del cambiamento.
Aggiungiamo quindi un pezzo nella nostra formula indicativo della rapidità:
Bene, ci siamo quasi. Abbiamo detto che il cambiamento di \(x\) deve essere minimo giusto!? E qual è lo strumento che usiamo per rappresentare qualcosa di infinitamente piccolo? Esatto proprio lui, il limite. La nostra \(h\) deve essere molto piccola, talmente tanto da essere quasi \(0\). Quindi scriviamo:
Questa funzione si chiama rapporto incrementale ed è la definizione matematica della derivata. Il suo segno, ci dice in che direzione cambia la funzione:
- se \(f'(x) > 0\): cresce e la funzione aumenta (rapidità positiva).
- se \(f'(x) < 0\): decresce e la funzione diminuisce (rapidità negativa).
- se \(f'(x) = 0\): rimane costante e la funzione non cambia.
Vediamo geometricamente cosa accade:
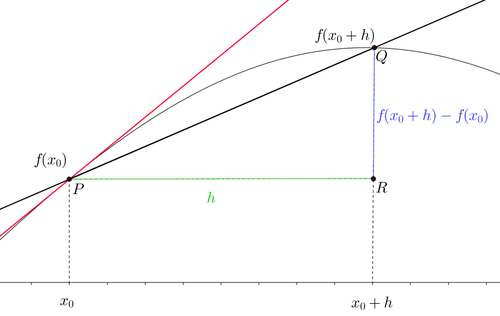Figura 1. Interpretazione Geometrica
La linea curva sottile è la nostra \(f(x)\). Come si può vedere, dato un valore \(x_0\) troviamo il punto \(P=(x_0, f(x_0))\). Se consideriamo l'aumento infinitesimo di \(h\), troviamo un secondo punto: \(Q=(x_0 + h, f(x_0 + h))\). Ora sono abbastanza sicuro (ho controllato questa mattina) che è ancora vero l'assioma che
Per due punti passa una, ed una sola, retta (almeno nella geometria Euclidea).
Questa retta è chiamata secante ed è la retta nera. Andiamo più in fondo e diamo una occhiata all'equazione della retta in forma esplicita:
dove \(m\) è il coefficiente angolare o pendenza della retta. Supponendo di conoscere due punti sulla retta, possiamo scrivere (se volete la dimostrazione, date uno sguardo qui):
Ma un momento, noi questi punti li abbiamo e sono:
e
Per cui scriviamo:
Vi ricorda qualcosa?!
Per cui quello che stiamo dicendo è che il rapporto incrementale altro non è che l'inclinazione della retta
secante. Quando \(h\) è infinitamente piccolo, quello che succede è che la distanza tra \(f(x_0+h)\) e \(f(x_0)\) diminuisce
al diminuire di \(h\). Questo vuol dire che \(Q\) si avvicina sempre di più a \(P\) fino a quando non diventano lo stesso punto.
Quindi, quando \(h\) tende a \(0\), come nella definizione di derivata, la secante diventa tangente che è quella rossa nel grafico. Tutto questo quindi ci porta a dire che il limite del rapporto incrementale, o
per gli amici la derivata, rappresenta l'inclinazione della retta tangente al grafico della funzione.
- Se la retta è inclinata verso l’alto da sinistra a destra allora \(f'(x) > 0\) e la funzione sta crescendo.
- Se è inclinata verso il basso da sinistra a destra allora \(f'(x) < 0\) e la funzione sta decrescendo.
- Se è orizzontale allora \(f'(x) = 0\) e la funzione è ferma.
L'inclinazione della retta ci dice infine la rapidità. Più la retta è ripida, maggiore è la rapidità del cambiamento. Se ad esempio considerassimo la funzione:
la sua derivata è:
Posto \(x=1\) abbiamo che
e
Il che vuol dire che nel punto
la funzione cresce con rapidità \(2\), cioè per ogni unità di incremento in \(x\), il valore di \(f(x)\) cresce di 2.
Ecco a voi una rappresentazione grafica di quanto detto:
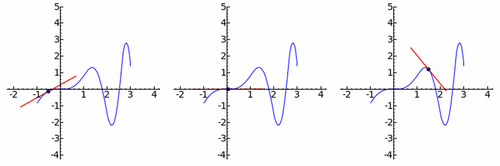Figura 2. Andamento Grafico Della Derivata
Da sinistra a destra potete vedere i tre casi: funzione crescente, funzione costante e funzione decrescente.
Sebbene ci sarebbe molto altro da dire sulle derivate, come le sue proprietà, mi limito ad aggiungere che da questo punto in poi non userò più la sola notazione \(f'(x)\) per indicare la derivata, ma anche la notazione \(\frac{d f}{d x}\) chiamata di Leibniz. Perché?! Perché sono sostenitore della paternità di Leibniz del calcolo differenziale...ma questa è un'altra storia. Vi basti sapere che sono notazioni alternative per rappresentare la medesima cosa.
Abbiamo dato quindi l'interpretazione matematica e geometrica della derivata, manca l'interpretazione fisica ma sinceramente non ho voglia, quindi beccatevi l'esempio sotto e vedetela lì.
Dalla Definizione all’Azione
Consideriamo un esempio molto semplice per meglio spiegare il concetto di derivata e il suo significato fisico. Supponiamo di essere in macchina e che la nostra posizione rispetto al tempo sia data da questa funzione:
Allora abbiamo:
Per cui:
Da cui:
Consideriamo infine il limite, dato che \(h \rightarrow 0\):
Abbiamo quindi calcolato la nostra derivata della funzione di spostamento. Ma cosa rappresenta?
Ricordiamo che la derivata misura la rapidità di variazione della funzione.
Nel nostro caso, rappresenta la rapidità con cui cambia la posizione nel tempo. Abbiamo quindi ottenuto la funzione velocità.
Analizziamola nel dettaglio, guardando il suo valore in diversi istanti di tempo:
- Supponiamo \(t=0\): \(\frac{d s}{d t} = 10\)
- Supponiamo \(t=5\): \(\frac{d s}{d t} = -10 + 10 = 0\)
- Supponiamo \(t=7\): \(\frac{d s}{d t} = -14 + 10 = -4\)
Nell'istante iniziale (caso 1) la velocità è di \(10 \frac{m}{s}\), ma passati \(5\) secondi (caso 2) siamo istantaneamente fermi. Questo vuol dire che la velocità sta diminuendo: stiamo decelerando. Superati i \(5\) secondi (caso 3), la velocità diventa negativa: stiamo tornando indietro, letteralmente. Quindi il comportamento della macchina era questo: si stava proseguendo in avanti ma decelerando, ci siamo fermati ed è iniziata la retromarcia.
Chi avrebbe detto che una semplice formula potesse raccontare così tanto? E indovina un po'? Abbiamo appena sfiorato la superficie.
Il Lato Oscuro della Variazione: L'Integrazione
La derivata è il cambiamento infinitesimo. Questo lo abbiamo detto e ridetto, e spero che il messaggio sia passato.
Ora fermiamoci un attimo a ragionare, se la derivata misura il cambiamento infinitesimo di una funzione allora, sommando
infiniti di questi piccoli cambiamenti, possiamo ricostruire la funzione originale.
Concettualmente torna, no?
Benissimo, questo che abbiamo appena presentato è il concetto di integrale. Attenzione però, perché qui le cose si fanno fetenti.
Infatti, mentre per le derivate abbiamo la formuletta analitica che ci aiuta, qui non c'è. Gli integrali sono una sorta di
pattern matching, la sua soluzione non è diretta bensì è conseguenza della domanda:
Quale è quella funzione che, derivata, mi restituisce quella che sto considerando?
Cioè per risolvere un integrale, lo dobbiamo riconoscere come derivata di qualcosa. Ma partiamo dall'inizio.
Nelle derivate, \(h\) rappresentava un incremento infinitesimo. Ora cambiamo notazione e non usiamo \(h\) ma usiamo \(dx\).
Abbiamo il cambiamento infinitesimo, quindi possiamo stimare quanto vale la variazione:
Dalla formula della derivata abbiamo
e quindi
Graficamente quello che stiamo calcolando è l'area di un rettangolo infinitesimo sotto la funzione \(f'(x)\), dove l'altezza è data dal dal valore di \(f'(x)\) in un dato punto, e la base è l' incremento infinitesimo \(dx\). Vi starete chiedendo perché ho usato il simbolo di approssimazione piuttosto che di uguaglianza. Guardate l'immagine che segue.
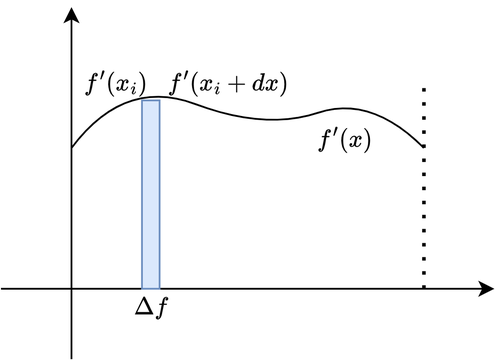Figura 3. Area Infinitesima
Come potete vedere il rettangolo non potrà mai calzare perfettamente una curva, ma più "stretto" è il rettangolo, ossia più piccolo è il \(dx\), migliore sarà l'approssimazione. E per \(dx \rightarrow 0\), l'approssimazione diventerà uguaglianza.
Come detto inizialmente, per risalire alla funzione originale, dobbiamo sommare tutte queste aree. E quante sono? Dato che l'incremento è infinitesimo è lecito pensare di avere infiniti incrementi. Quindi possiamo scrivere:
Questa somma è una approssimazione, e portata all'infinito diventa l'integrale. Matematicamente, si indica così:
Questa formula rappresenta il teorema fondamentale del calcolo integrale e ci dice, in parole povere, che l'integrale è l'operazione inversa della derivata. La generica \(F(x)\) si chiama primitiva ed è la funzione la cui derivata, restituisce l'argomento (ciò che integriamo) dell'integrale.
Ora vi starete chiedendo: cosa diamine è questa C?
Se applicate la formula del rapporto incrementale a una funzione costante, otterrete \(0\). Questo vuol dire che
derivando perdiamo tutte le informazioni sulle costanti. Ecco perché quando integriamo, dobbiamo sempre aggiungere
la costante \(C\), per compensare questa perdita di informazione.
Abbiamo appena definito quello che si chiama integrale indefinito. E sì, se esiste quello indefinito esiste anche quello definito. L'integrale definito calcola non una funzione ma un numero e si indica così:
Cioè la differenza tra la primitiva calcolata in \(b\) e in \(a\).
Quella che avete appena avuto il "piacere" di leggere è l'integrazione di Riemann. Ce ne sono tante altre come ad esempio quella di
Lebesgue, ma tranquilli non la vediamo che mi sono stancato io, immagino voi.
Ora abbiamo tutto l'occorrente per due esempi.
Integrale Indefinito
Supponiamo di avere
e di voler risalire alla \(f(x)\), si ha:
Come ci si arriva?
Il processo mentale deve essere: qual è quella funzione che, derivata, mi restituisce \(x\)?
Applichiamo il rapporto incrementale alla \(f(x)\) ottenuta e vediamo che funziona!
Per concludere questo esempio, la \(f(x)\) di partenza poteva essere semplicemente \(\frac{(x+h)^2}{2}\) o anche \(\frac{(x+h)^2}{2} + 1\) o ancora \(\frac{(x+h)^2}{2} + 100000\). I valori costanti vanno sempre persi nel calcolo della derivata. Quindi, quando con l'integrale passiamo da una funzione derivata alla primitiva, è necessario considerare queste costanti con una generica \(C\). Pena, un punto in meno su un esercizio da cinque. Fidatevi...
Integrale Definito
Per questo secondo esempio, oltre che ad applicare la formula dell'integrale voglio mostrarvi anche perché l'idea della somma infinita dell'area dei rettangoli, funziona.
Supponiamo di voler calcolare l'area sotto la funzione \(f(x) = 2x\) in \([0, 2]\).
Da notare che non c'è il simbolo di derivata. Questo perché le derivate
sono il classico consulente in shadow: ci sono fanno tutto ma non li vedi e non li senti (tranquilli, neanche loro vogliono vedervi e sentirvi).
Torniamo a noi. Usando l'integrale in senso stretto, la tavola degli integrali indefiniti
ci aiuta e scriviamo:
Quindi l'area tra \([0, 2]\) sotto la funzione \(f(x) = 2x\) è \(4\) e il problema sarebbe già risolto.
Dato che però sono infame, ora applichiamo strettamente la teoria e facciamo questa maledetta somma infinita.
Siamo nell'insieme \([0, 2]\) e lo vogliamo dividere in tanti pezzettini infinitesimi \(dx\). Naturalmente usiamo la divisione e possiamo scrivere:
dove \(n \rightarrow \infty\) cioè \(n\) è talmente grande che abbiamo infiniti pezzettini (o rettangoli) del range di interesse.
Un pezzettino di area è quindi:
e sommando tra di loro tutte queste aree abbiamo:
Ora attenzione a questo passaggio. Dobbiamo considerare ogni punto sul grafico di \(2x_i\). Questo stesso grafico però è diviso in tanti \(dx\), come visto prima. Il primo di questi rettangoli avrà estremi in \([0, dx]\), il secondo in \([dx, 2dx]\), e così via. Ma abbiamo detto che ogni \(dx\) è il risultato di \(\frac{2}{n}\) giusto?! Per cui sostituendo a prima abbiamo che il primo rettangolo sarà in \([0, \frac{2}{n}]\), il secondo in \([\frac{2}{n}, 2 \cdot \frac{2}{n}]\), e così via. Avete notato il pattern? Vi prego ditemi di sì perché non saprei come altro dirlo... Per farla breve quindi, abbiamo che i punti della base del rettangolo seguono la legge:
Per meglio rendere l'idea vedete l'immagine che segue:
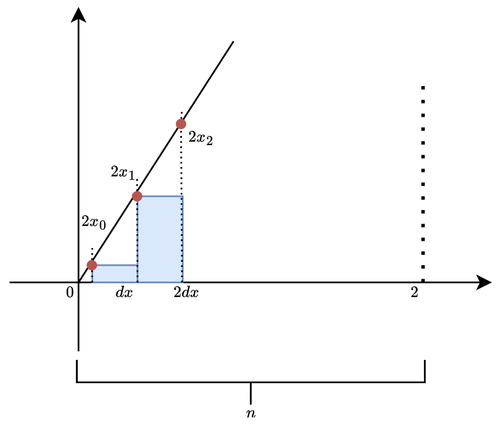Figura 4. Partizionamento Dominio
Quindi facendo delle sostituzioni possiamo vedere quanto vale \(f(x_i)\) in ogni punto:
- In \(i=0\) \(2x_i = 2 \cdot 0 \cdot \frac{2}{n} = 0\)
- In \(i=1\) \(2x_i = 2 \cdot 1 \cdot \frac{2}{n} = \frac{4}{n}\)
- In \(i=2\) \(2x_i = 2 \cdot 2 \cdot \frac{2}{n} = \frac{8}{n}\)
- ...
Tornando quindi alla nostra sommatoria, è lecito sostituire
con il suo valore in ogni punto che è
da cui:
come si vede l'unica variabile legata alla sommatoria è \(i\). Per risolverla quindi vanno sommati infiniti \(i\):
E quanto vale questa somma? Se avete studiato analisi e non lo sapete dovreste solo vergognarvi. Per tutti gli alti sappiate che ha una soluzione ben dimostrata dal buon Gauss, da cui:
quindi abbiamo
ma vi ricordo che \(n\) tende a infinito per cui scriviamo:
Abbiamo ottenuto esattamente lo stesso risultato.
Ve lo avevo detto o no che l'integrale è la somma di infinite aree di rettangoli!?
Cosa?! Anche ora volete una (non richiesta) interpretazione fisica? Bene, vi ricordare quando abbiamo detto che la velocità è
la derivata dello spazio rispetto al tempo? Bene, dato che l'integrale è l'inverso della derivata, integrando la velocità (sì, siamo in presenza della funzione velocità) rispetto
al tempo, otteniamo la funzione spazio. Ed infatti se viaggiassimo alla velocità di \(2t\) per \(2\) secondi, quanto spazio percorreremmo? Esatto
proprio \(4\) metri.
Quando il Cambiamento Diventa Legge
Ok, ora il gioco si fa serio, ma manteniamo la calma.
Nel paragrafo precedente abbiamo osservato la derivata come lo strumento principe per misurare come cambia una funzione nel tempo.
Abbiamo anche visto che, conoscendo una derivata, possiamo (almeno in teoria) risalire alla funzione originale tramite l’integrale.
Ma cosa succede se, invece di avere una derivata “pulita”, pronta da integrare, abbiamo una regola che ci dice come quella derivata si comporta,
magari anche in funzione della stessa variabile? In altre parole: e se conoscessimo solo un'equazione che collega il tasso di cambiamento
alla funzione stessa, senza conoscere né l’una né l’altra? Benvenuti nel regno delle equazioni differenziali ordinarie, o per gli amici: ODE.
Le ODE non ci dicono che faccia ha una funzione, ma come evolve nel tempo. Non sono l’identikit del fenomeno, ma il suo comportamento dinamico.
E attenzione: non fatevi trarre in inganno dalla parola “equazione”. Se in un’equazione algebrica cerchiamo un numero, in una ODE la
risposta è un’intera funzione. E' doveroso dire che quando si parla di equazioni differenziali, si parla di un
mondo di cui le ODE sono solo una piccolissima parte. Ci sono le PDE (equazioni differenziali alle derivate parziali), le SDE (equazioni differenziali stocastiche)
e via dicendo. Ed ognuna a modo suo ti fa del male. Molto del male. Ma dato che sono ancora troppo giovane per rimanerci secco,
al momento concentriamoci sulle ODE e chi vivrà, vedrà.
Ma che aspetto ha una ODE? Una ODE è come il covid... non la vediamo e non la sentiamo, ma è lì che ci minaccia e qualcuno ne nega l'esistenza.
In sostanza, è un’equazione che coinvolge almeno una derivata e che ci dice come qualcosa deve cambiare. Tutto gira attorno a una sola variabile indipendente
che di solito è il tempo \(t\) (ma potrebbe anche essere lo spazio, la temperatura o quanta voglia di vivere hai).
Invece di conoscere direttamente una funzione \(y(t)\) conosciamo la sua derivata, ossia come \(y(t)\) stessa cambia nel tempo.
Partiamo dall'esempio più semplice di ODE:
Dove:
- \(t\) è la variabile indipendente (spesso il tempo),
- \(y\) è la funzione incognita che vogliamo trovare,
- \(f(y(t), t)\) è la funzione che descrive come \(y(t)\) cambia nel tempo.
Facciamo un esempio:
Come potete vedere non sappiamo quale è la funzione \(y(t)\), ma quello che sappiamo è che \(y\) cresce proporzionalmente al proprio valore con un fattore \(3\). L'obiettivo quindi, è calcolare la funzione \(y(t)\) che soddisfa questa legge di crescita. In questo caso, la soluzione è:
Come ho fatto a trovarla lo scopriremo...
Per il momento limitiamoci a dare qualche altra chicca sulle ODE. Quella che abbiamo appena visto è un' equazione differenziale ordinaria di primo grado, lineare, esplicita a coefficienti costanti.
- Con primo grado si intende che compare solo la prima derivata \(\frac{dy}{dt}\), e non derivate superiori come \(\frac{d^2y}{dt^2}\).
- Con lineare si intende che la funzione \(y\) e le sue derivate appaiono al primo grado (cioè non ci sono potenze, prodotti o funzioni non lineari di \(y\)).
- Con esplicita si intende che la derivata è isolata da un lato dell’equazione, nella forma classica: \(\frac{dy}{dt} = f(t, y)\).
- Con coefficienti costanti si intende che i termini moltiplicativi che accompagnano \(y\) o le sue derivate non dipendono dalla variabile indipendente \(t\), ma sono numeri fissi.
Dato che ora sapete come è fatta una ODE carina e coccolosa. Per par condicio, vediamone una che fa bestemmiare:
Qui abbiamo tutto il contrario:
- E' di secondo grado, vuol dire che la \(y(t)\) è stata derivata due volte come si vede dal termine \(\frac{d^2y}{dt^2}\).
- E' non lineare dato che la \(y\) è al quadrato.
- E' implicita perché la derivata ha un fattore moltiplicativo \(t\).
- E' a coefficienti variabili perché la \(y\) e/o le sue derivate sono moltiplicate per un valore variabile e non costante.
Come ti Senti: Mah, Cauchy Cauchy...
Prima ho scritto che la soluzione di una ODE è una funzione, e questo è vero. Ma non ho mai detto che non è possibile sapere quanto vale la nostra \(y(t)\) in un determinato istante \(t\). Tutto quello che ci serve è un punto di innesco cioè ci serve sapere, almeno in un istante \(t\), quanto vale \(y(t)\). Sapendo questo, possiamo sapere quanto vale ovunque. Questo punto di innesco si chiama condizione iniziale e se lo abbiamo, siamo in presenza di un Problema di Cauchy o un IVP (Initial Value Problem). In IVP è strutturato in questo modo:
Cioè stiamo dicendo che, una volta risolta la ODE, sappiamo che nell'istante \(t=k\), \(y(t)\) vale \(z\).
Da Legge a Sistema
Purtroppo (o per fortuna) il mondo non funziona con una sola variabile. Quando vogliamo descrivere più fenomeni che interagiscono, dobbiamo abbandonare l'equazione singola e passare ai sistemi di ODE. Un sistema di ODE è un insieme di equazioni che descrive più grandezze in evoluzione, tutte legate tra loro. Ad esempio:
Qui le funzioni \(x(t)\) e \(y(t)\) si influenzano a vicenda. Non basta risolverne una e poi l'altra: sono accoppiate, vanno risolte insieme. Anche in presenza di un sistema, avendo le condizioni iniziali di entrambe le ODE, siamo in presenza di un IVP.
ODE Hall of Fame
Si, so che fino a qui è stato tutto particolarmente complicato e astratto, ma anche se così non sembra sappiate che siamo circondati da ODE. ODE ovunque. Un esempio?! La celebre formula, o secondo principio della dinamica di Newton (si dai, non diamo tutti i meriti a Leibniz)
Anche se così non sembra, l'accelerazione è la derivata della velocità che a sua volta è la derivata dello spazio rispetto al tempo. Quindi l'accelerazione è la derivata seconda dello spazio rispetto al tempo e possiamo scriverla come:
Altro esempio celebre è il sistema di Lotka-Volterra o modello preda-predatore. Questo sistema di ODE rappresenta l'equilibrio che si crea in un ambiente dove ci sono prede e predatori (ad esempio conigli e volpi). Il sistema è il seguente:
L'andamento grafico di questo sistema è riportato nel diagramma che segue chiamato di direzione e fase
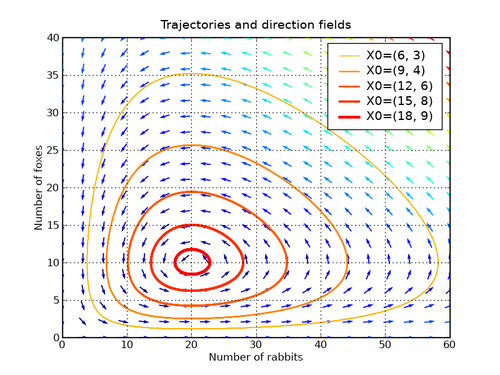Figura 5. Lotka-Volterra Direzione e Fase
C'è da precisare che i due grafici sono rappresentabili separatamente ma per velocità di esposizione ve li beccate insieme. Il grafico di direzione, si usa per le sole ODE di primo grado e rappresenta visivamente come si comportano le soluzioni in ogni punto del piano, associandoci una freccia tangente alla curva che attraversa quel punto. Ora sapete che mostra, quindi, non solo la direzione ma anche la velocità di cambiamento della ODE. Se non vi è chiaro il perché, non me lo dite, altrimenti vorrebbe dire che tutto quello scritto è stato inutile.
Il diagramma di fase invece, è usato per sistemi di ODE e rappresenta l’evoluzione delle relazioni tra variabili. Tornando al grafico, \(x\) e \(y\) sono volpi e conigli e come si vede l'interazione tra di loro è un sistema chiuso. Al crescere delle volpi, essendoci troppi predatori, i conigli diminuiscono e quando diminuiscono troppo, non c'è abbastanza cibo per tutti i predatori che cominceranno anch'essi diminuire dando modo ai conigli di ripopolarsi. Le diverse linee colorate rappresentano lo stesso sistema, quindi lo stesso comportamento, ma con diverse condizioni iniziali.
Andiamo avanti e vediamo l'ultima celebre ODE della giornata. Avete mai sentito parlare dell'effetto farfalla? Quell'idea secondo cui le piccole azioni, possano portare a grandi e imprevedibili conseguenze a lungo termine. Bene, quell'effetto nasce proprio dal sistema di ODE che segue, chiamato sistema di Lorenz:
E il suo grafico è il seguente:
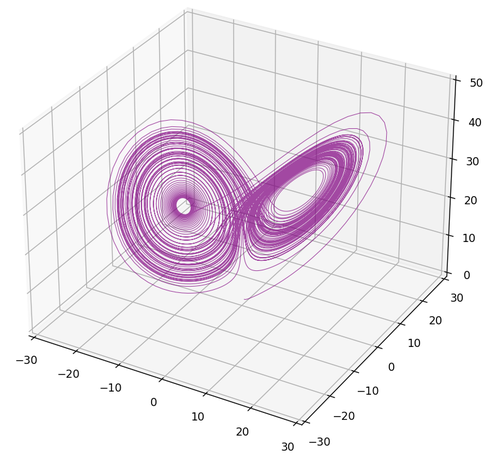Figura 6. Attrattore Lorenz Fase
Dal suo andamento potete intuire perché si chiama effetto farfalla, ma le cose interessanti di questo sistema di ODE sono altre. Come ad esempio il fatto che il grafico non passa mai due volte sulla stessa traiettoria. Inoltre, essendo che le variabili si influenzano a vicenda con fattore moltiplicativo, una piccolissima variazione cresce di molto con il passare del tempo \(t\), ed è per questo che è associato al caos. Ultimo punto degno di nota è la presenza di attrattori, cioè dei punti che richiamano a loro le soluzioni delle ODE. Anche se, come i fulmini, il sistema di Lorenz non passa mai due volte sullo stesso punto, il sistema stesso è attratto da quei punti orbitandoci intorno. Un sistema con comportamento inverso si chiama repulsore e può essere visto nel grafico sottostante.
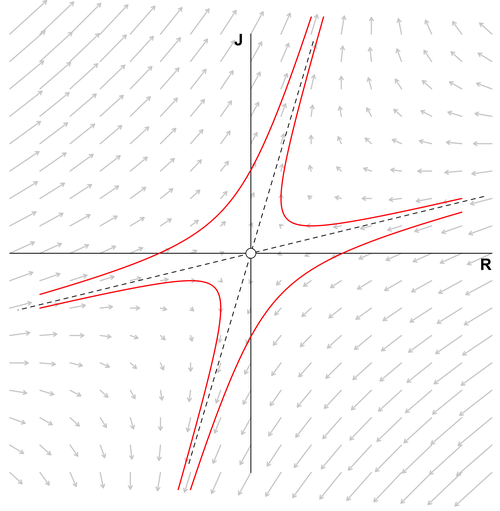Figura 7. Repulsore
Ora però concludo il paragrafo che sta arrivando un temporale.
Conclusioni
So che questo articolo è stato matematicamente un po' pesante, e che di informatica, reti neurali e metaeuristica non c'è nulla. Ma hey, se l'ho messo nella sezione Teoria e Matematica ci sarà pure un motivo, no? Purtroppo, che vi piaccia o meno la matematica che vi si nasconde dietro, è questa. E se siete del tipo:
ooooh si che bello, le intelligenze artificiali ci lavoro e mi piacciono un casino, amoooo...
e poi, odiate la matematica e la conoscenza più approfondita che avete a riguardo si riassume in import sklearn, avete proprio sbagliato
mestiere. Polemiche a parte, non vi adagiate sugli allori dicendo:
sono arrivato alla fine
perché non è finita affatto. C'è molto altro da dire, come ad esempio:
Come minchia si risolvono le ODE?
Ma dato che questo è uno di una serie di articoli, rimandiamo la risposta ai prossimi e mandiamo giù questo amaro boccone. Nel frattempo però, potete andare su questo repo per vedere all'azione, alcuni degli argomenti trattati.
Alla Prossima.