Io ODO, Tu ODI e la Neural ODE

C'è un momento nella vita di ogni matematico, ingegnere e figure mitologiche simili, in cui

Ti piace l'analitica eh!? Allora beccati sta ODE.

E te ne sbatte in faccia una non lineare, accoppiata, implicita, con coefficienti che cambiano neanche fossero le scale di Hogwarts. L'unica cosa che puoi farci è non risolverla. Nemmeno pregando le buon anime di Gauss, Leibniz e altri matematici che veneri. O meglio questo era vero fino alla nascita dei metodi numerici. Poco eleganti, spesso sporchi, ma tremendamente efficaci. Non ti danno formule chiuse con cui vantarti, ma se ti accontenti del risultato approssimato non hai proprio di che lamentarti. Del resto, anche se non si direbbe, siamo circondati da approssimazioni: quando usate Google Maps (che vi dice che arriverete tra 10 minuti e ce ne mettete 17), quando mettete un pizzico di sale (dove il "pizzico" è un cucchiaio da cucina), quando leggete il mio blog (che dovrebbe essere divulgativo invece aiuta più me a ricordare che voi a imparare)...

Ma bando agli indugi, dato che non state più nella pelle vediamo questi famosi metodi numerici. Ma prima, se non l'hai fatto, recupera la Parte 1 e la Parte 2.

ODE a Piccoli Passi

Riprendiamo il tanto decantato sistema di Lotka-Volterra introdotto qui.

$$ \begin{cases} \frac{dx}{dt} = \alpha x - \beta x y \\ \frac{dy}{dt} = \delta x y - \gamma y \end{cases} $$

dove:

$x(t)$ è il numero di prede (es. conigli).
$y(t)$ è il numero di predatori (es. volpi).
$\alpha$ è il tasso di crescita delle prede. Descrive quanto velocemente si riproducono le prede in assenza di predatori (che nei conigli sembra essere alto come vuole la leggenda).
$\beta$ è il tasso di predazione. Dice quanto le prede vengono uccise dai predatori.
$\delta$ è il tasso di conversione. Dice quanti nuovi predatori nascono ad ogni preda mangiata e digerita.
$\gamma$ è il tasso di mortalità dei predatori. Rappresenta la morte naturale dei predatori in assenza di prede. Se non mangiano muoiono di fame.

Non c'è un metodo analitico noto per risolvere simbolicamente questo sistema quindi ricorriamo ai metodi numerici. Sono strategie per ottenere una soluzione approssimata, per passi piccoli, discreti e speranzosi. Tutto nasce grazie al sommo Eulero che, oltre a regalarci il famosissimo tatuaggio

$$ e^{i \pi} + 1 = 0 $$

(no serio ragà, smettete di tatuarvelo se non sapete manco cos’è il pi greco), ci ha dato anche il capostipite di tutti i metodi numerici: il metodo di Eulero. La convergenza di questo metodo è stata dimostrata dal sommo Cauchy ed è stato poi generalizzato dai sommi Runge e Kutta con la famiglia dei metodi RK. Insomma qui tutti sono sommi e il mondo dei metodi numerici è più affollato dell'algoritmo di TikTok. Ce ne sarebbero tanti altri da affrontare ma ci limiteremo solo ad alcuni.

Metodo Di Eulero

Riprendiamo la formula dell'espansione di Taylor. Ricordi? Ne ho già parlato qui. La serie di Taylor è un po' un jolly, si usa ovunque.

Consideriamo in particolare una espansione al primo ordine cioè del tipo

$$ f(x) = f(a) + f'(a) \cdot (\bar x) + O(\bar x^2) $$

dove

$$ \bar x = (x - a) $$

cioè stiamo valutando la funzione in $x$, considerando le derivate in un punto distante $a$ da $x$ stesso. Consideriamo ora un generico problema di Cauchy

$$ \begin{cases} y'(t) = f(y(t), t) \\ y(t_0) = y_0 \end{cases} $$

e consideriamo la definizione di derivata. Possiamo scrivere, per $h \rightarrow 0$:

$$ y'(t) \approx \frac{y(t+h) - y(t)}{h} $$

$$ \Rightarrow h \cdot y'(t) \approx y(t+h) - y(t) $$

$$ \Rightarrow y(t+h) \approx y(t) + h \cdot y'(t) $$

Vi ricorda qualcosa? Esatto proprio uno sviluppo di Taylor al primo ordine ma dove:

$x = t + h$
$a = t$

Cioè calcoliamo la derivata nel punto $t$ e valutiamo lo sviluppo nel punto $t+h$. Ora facciamo un altro sforzo e supponiamo di partire dal punto $t_0$ che è noto dato che, vi ricordo, siamo in un problema di Cauchy. Facciamo un passettino infinitesimo $h$ in avanti e finiamo nel punto $t_1$. Per cui scriviamo

$$ y(t_1) = y(t_0 + h) \approx y(t_0) + h \cdot y'(t_0) $$

dove

$$ t_1 = t_0 + h $$

Una volta che conosciamo $t_1$, possiamo andare in $t_2$ con lo stesso principio

$$ y(t_2) = y(t_1 + h) \approx y(t_1) + h \cdot y'(t_1) $$

dove

$$ t_2 = t_1 + h = t_0 + 2h $$

Capita l'antifona? Possiamo quindi generalizzare in questo modo

$$y(t_{n+1}) = y(t_n + h) \approx y(t_n) + h \cdot y'(t_n)$$

Formula 1. Sviluppo della ODE di Ordine Uno

Quindi

$$t_{n+1} = t_n + h = t_0 + n \cdot h$$

Formula 2. Discretizzazione del Tempo

Dove:

$t_0$ è l'istante iniziale
$t_{n+1}$ è l'istante finale
$h$ è il passo di integrazione, scelto a piacere
$n$ è il numero di iterazioni

In pratica stiamo discretizzando il tempo. Più $h$ è piccolo, più il metodo è accurato ma computazionalmente oneroso.

Riprendiamo ora il problema di Cauchy e abbiamo:

$$ y'(t) = f(y(t), t) $$

e quindi possiamo sostituire $y'(t)$ nel metodo di Eulero, ottenendo la formulazione finale:

$$y(t_{n+1}) \approx y(t_n) + h \cdot f(y(t_n), t_n)$$

Formula 3. Metodo di Eulero Esplicito

Quella scritta è la formula del Metodo di Eulero Esplicito. Perché esplicito? Perché usiamo tutti valori che conosciamo già. Infatti supponiamo di voler calcolare $y(t_1)$, dovremmo calcolare:

$y(t_0)$ che è il valore noto del problema di Cauchy
$f(y(t_0), t_0)$ calcolabile tramite semplice sostituzione di valori

Se esiste il metodo esplicito ovviamente esiste anche l'implicito la cui formula, omettendo la dimostrazione, è:

$$y(t_{n+1}) \approx y(t_n) + h \cdot f(y(t_{n+1}), t_{n+1})$$

Formula 4. Metodo di Eulero Implicito

E' implicito perché, come potete vedere, il valore da calcolare $t_{n+1}$ compare in entrambi i lati dell'equazione. Non sempre si risolve con facilità. In determinati casi, sono necessari metodi iterativi come il metodo delle sostituzioni successive. Ma questo esula questo articolo quindi, dato che la vita ce la siamo già complicati abbastanza, vi lascio alla vostra volontà di approfondire.

Esempio Eulero

Tutto troppo teorico fino ad ora lo so, quindi vediamo qualcosa di pratico con un esercizio. Consideriamo il seguente problema di Cauchy rappresentante il decadimento esponenziale. Sembra fine a se stesso, in realtà molti fenomeni naturali seguono questa legge come il decadimento radioattivo, la scarica del condensatore nei circuiti RC...

$$ \begin{cases} y' = -ky \\ y(t_0) = 1 \\ k = 1 \end{cases} $$

dove $k$ è il tasso di decadimento e, in questo caso, lo scegliamo noi. La soluzione della ODE è:

$$ y(t) = e^{-1 \cdot t} $$

Se volete i passaggi fateveli. Conoscete gli strumenti per risolverla. Per l'esempio ho scelto questa ODE (che è risolvibile analiticamente come avete visto), per poter mostrare la differenza tra una soluzione esatta e una numerica. Vediamo quanto vale nei punti $t=1, \text{ } t=2$

$$ \begin{array}{|c|c|c|} \hline t & y(t) & \text{Result} \\ \hline 0 & e^0 & 1 \\ \hline 1 & e^{-1 \cdot 1} & 0.367 \\ \hline 2 & e^{-1 \cdot 2} & 0.135 \\ \hline \end{array} $$

Ora risolviamo con il metodo di Eulero. Dalla formula di discretizzazione del tempo sappiamo già quanti sono gli step da fare posto $h=0.1$, istante iniziale $t_0=0$ e istante finale $t_{n}=2$:

$$ t_{n} - t_0 = n \cdot h \Rightarrow 2-0 = n \cdot h \Rightarrow n = 20 $$

Per chiarezza di esposizione, eseguiamolo step by step. Il valore in $t_0$ è noto dal problema di Cauchy, quindi:

Passo $n=1$
$$ t_{1} = t_0 + 1 \cdot 0.1 = 0.1 $$

$$ y(t_1) \approx y(t_0) + h \cdot f(y(t_0), t_0) $$

$$ y(0.1) \approx y(0) + 0.1 \cdot f(y(0), 0) $$

$$ y(0.1) \approx 1 + 0.1 \cdot (-1 \cdot 1) = 0.9 $$

Passo $n=2$

$$ t_2 = t_0 + 2 \cdot 0.1 = 0.2 $$

$$ y(t_2) \approx y(t_1) + h \cdot f(y(t_1), t_1) $$

$$ y(0.2) \approx y(0.1) + 0.1 \cdot f(y(0.1), 0.1) $$

$$ y(0.2) \approx 0.9 + 0.1 \cdot (-1 \cdot 0.9) = 0.81 $$

E così via. Fidatevi quando vi dico che i risultati sono quelli riportati in questa tabella:

$$ \begin{array}{|c|c|c|} \hline n & t_n & \text{Result} \\ \hline 0 & 0 & 1 \\ \hline 1 & 0.1 & 0.9 \\ \hline 2 & 0.2 & 0.810 \\ \hline \dots & \dots & \dots \\ \hline 10 & 1 & 0.349 \\ \hline \dots & \dots & \dots \\ \hline 20 & 2 & 0.122 \\ \hline \end{array} $$

Ora vediamo che succede ponendo $h=0.5$. Non lo farò step by step perché ora sapete come si fa, quindi beccatevi sta tabella:

$$ \begin{array}{|c|c|c|} \hline n & t_n & \text{Result} \\ \hline 0 & 0 & 1 \\ \hline 1 & 0.5 & 0.5 \\ \hline 2 & 1 & 0.250 \\ \hline 3 & 1.5 & 0.125 \\ \hline 4 & 2 & 0.062 \\ \hline \end{array} $$

Ecco un confronto sintetico tra la soluzione analitica e le due approssimazioni numeriche:

$y(t)$ soluzione analitica
$E(h=0.1)$ Eulero con $h=0.1$
$E(h=0.5)$ Eulero con $h=0.5$

$$ \begin{array}{|c|c|c|c|} \hline t & y(t) & E(h=0.1) & E(h=0.5) \\ \hline 0 & 1 & 1 & 1 \\ \hline 1 & 0.367 & 0.349 & 0.25 \\ \hline 2 & 0.135 & 0.122 & 0.062 \\ \hline \end{array} $$

Come potete vedere, al netto di $n=0$ che è la soluzione nota, $h=0.1$ approssima molto meglio rispetto a $h=0.5$ ma ha richiesto $20$ passi rispetto ai $4$ del secondo.

Quanto detto può essere riassunto dalla seguente immagine

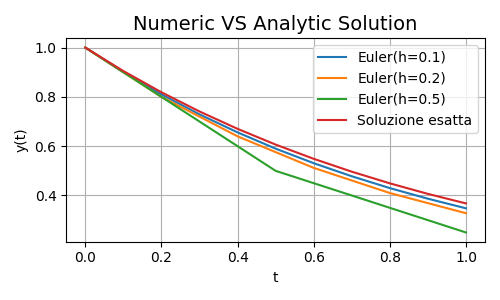Comparison Figura 1. Comparazione Risultati

La soluzione esatta è quella rossa, e al diminuire di $h$ l'approssimazione è via via migliore. Bene, è il momento di passare al prossimo round dove i Runge-Kutta vi stenderanno.

La Famiglia Mans... RK

Diamo a Cesare quel che è di Cesare, il metodo di Eulero è il patriarca di tutti i metodi numerici. Ma è davvero così buono? Beh come sempre... dipende. Ad esempio dal vostro tipo di problema. Per problemi troppo complessi fallisce miseramente. Quindi è buono e caro ma diciamocelo, non ha più l'età. C'è bisogno di carne fresca, di giovini pavidi e forti. Arriviamo così ai metodi Runge Kutta o RK.

I metodi RK sono una famiglia neocatecumenale, ce ne sono tanti, ed ognuno ha le sue peculiarità. L'unica cosa certa, oltre la morte, è che mantengono la stessa idea di base di Eulero. Procedere per piccoli passi.

Ripartiamo dalla formula di Taylor. Come ben ricorderete maggiore è lo sviluppo, migliore è l'approssimazione. I metodi RK si basano proprio sullo sviluppo di ordini superiori della serie di Taylor. Eulero quindi può essere visto come un metodo RK1 cioè Runge Kutta del primo ordine. Vediamo cosa succede se non ci accontentiamo del primo ordine ed arriviamo al secondo, partendo dalla Formula del Primo Ordine:

$$y(t_{n+1}) = y(t_n + h) \approx y(t_n) + h \cdot y'(t_n) + \frac{h^2}{2} \cdot y''(t_n)$$

Dato che

$$ y'(t_n) = f(y(t_n), t_n) $$

$$ \Rightarrow y''(t_n) = f'(y(t_n), t_n) $$

$$\Rightarrow y(t_{n+1}) \approx y(t_n) + h \cdot f(y(t_n), t_n) + \frac{h^2}{2} \cdot f'(y(t_n), t_n)$$

Formula 5. Sviluppo della ODE di Ordine Due

Possiamo quindi utilizzare la definizione della derivata prima e sviluppare il rapporto incrementale di $f'$:

$$ f'(y(t_n), t_n) \approx \frac{f(y(t_n + h), t_n+h) - f(y(t_n), t_n)}{h} = \frac{f(y(t_{n+1}), t_{n+1}) - f(y(t_n), t_n)}{h} $$

Ma da Eulero sappiamo che

$$ y(t_{n+1}) = y_{n+1} = y_n + h \cdot f(y_n, t_n) $$

per cui, sostituendo:

$$ f'(y_n, t_n) \approx \frac{f(y_n + h \cdot f(y_n, t_n), t_{n+1}) - f(y_n, t_n)}{h} $$

Sostituendo ancora, nella formula dello Sviluppo di Ordine Due abbiamo:

$$ y_{n+1} \approx y_n + h \cdot f(y_n, t_n) + \frac{h}{2} \cdot \left [ f(y_n + h \cdot f(y_n, t_n), t_{n+1}) - f(y_n, t_n) \right] $$

$$ \Rightarrow y_{n+1} \approx y_n + \frac{h}{2} \cdot \left [ f(y_n + h \cdot f(y_n, t_n), t_{n+1}) + f(y_n, t_n) \right] $$

Quindi posti:

$$ k_1 = f(y_n, t_n) \\ k_2 = f(y_n + h \cdot f(y_n, t_n), t_{n+1}) = f(y_n + h \cdot k_1, t_{n+1}) $$

troviamo il cosiddetto Metodo RK2 o Metodo di Heun

$$ \begin{cases} k_1 = f(y_n, t_n) \\ k_2 = f(y_n + h k_1, t_n + h) \\ y_{n+1} \approx y_n + \frac{h}{2} (k_1 + k_2) \end{cases} $$

Formula 6. Metodo di Heun

Con la stessa logica, si possono calcolare ordini superiori sviluppando ulteriormente la serie di Taylor:

RK3 o Shu-Osher
RK4
RK5 o Dormand-Prince
... e tanti altri.

Data la sua importanza, non si può non riportare la formulazione di RK4 che è un ottimo compromesso tra precisione e complessità computazionale:

$$ \begin{cases} k_1 = f(y_n, t_n) \\ k_2 = f(y_n + \frac{h}{2} k_1, t_n + \frac{h}{2}) \\ k_3 = f(y_n + \frac{h}{2} k_2, t_n + \frac{h}{2}) \\ k_4 = f(y_n + h k_3, t_n + h) \\ y_{n+1} \approx y_n + \frac{h}{6} (k_1 + 2k_2 + 2k_3 + k_4) \end{cases} $$

Formula 7. Metodo RK4

Da notare che, sempre perché vi voglio bene, abbiamo considerato unicamente i metodi espliciti, ma solo perché abbiamo la testa sotto la sabbia non vuol dire che quelli impliciti (perché sì, esistono gli RK impliciti) non possano farvi del male.

Esempio RK

Se siete arrivati qui avrete sentito millanta volta Lotka-Volterra. Dato che ora possiamo, perché non risolverlo?! Consideriamo quindi la seguente istanza:

$$ \begin{cases} \frac{dx}{dt} = \alpha x - \beta x y \\ \frac{dy}{dt} = \delta x y - \gamma y \\ \alpha = 1.1 \\ \beta = 0.4 \\ \delta = 0.1 \\ \gamma = 0.4 \\ x_0 = 10 \\ y_0 = 5 \end{cases} $$

ovviamente, data tutta la paturnia sopra, usiamo i metodi numerici con

$$ h=0.1 \\ t \in [0, 2] $$

in particolare sviluppiamo per Heun e RK4. Tranquilli, è giusto per farvi vedere come funzionano quindi svilupperemo solo per un passo.

Heun, $n=1$

Vi ricordo che Lotka-Volterra è un sistema di due ODE, quindi la faccenda si complica un pochino ma nulla di astruso, niente panico. Iniziamo calcolando $k_1$ e $k_2$. Dato che le ODE sono due, sono calcoleremo

$k_1^x, k_2^x$ per la prima ODE
$k_1^y, k_2^y$ per la seconda ODE

$$ k_1^x = \alpha x_0 - \beta x_0 y_0 \\ k_1^y = \delta x_0 y_0 - \gamma y_0 $$

$$ k_2^x = \alpha (x_0 + h k_1^x) - \beta (x_0 + h k_1^x) \cdot (y_0 + h k_1^y) \\ k_2^y = \delta (x_0 + h k_1^x) \cdot (y_0 + h k_1^y) - \gamma (y_0 + h k_1^y) $$

$$ x_1 = x_0 + \frac{h}{2} (k_1^x + k_2^x) \\ y_1 = y_0 + \frac{h}{2} (k_1^y + k_2^y) $$

Sostituendo:

$$ k_1^x = 1.1 \cdot 10 - 0.4 \cdot 10 \cdot 5 = 11 - 20 = -9 \\ k_1^y = 0.1 \cdot 10 \cdot 5 - 0.4 \cdot 5 = 5 - 2 = 3 $$

$$ k_2^x = 1.1 \cdot (10 - 0.1 \cdot 9) - 0.4 \cdot (10 - 0.1 \cdot 9) \cdot (5 + 0.1 \cdot 3) \approx 10.01 - 19.292 = -9.282 \\ k_2^y = 0.1 \cdot (10 - 0.1 \cdot 9) \cdot (5 + 0.1 \cdot 3) - 0.4 \cdot (5 + 0.1 \cdot 3) \approx 4.823 - 2.12 = 2.703 $$

$$ x_1 = 10 + 0.05 \cdot (-9 - 9.282) = 9.086 \\ y_1 = 5 + 0.05 \cdot (3 + 2.703) = 5.285 $$

I più attenti di voi si chiederanno perché $t+h$, che è richiesto per il calcolo di $k_2$, di fatto non appare mai. Presto detto, tutte le ODE del sistema, non dipendono esplicitamente dalla variabile tempo $t$, quindi è ininfluente ai fini del calcolo; ma se fosse apparso, il tempo corrente è quello calcolato tramite la Formula di Discretizzazione del Tempo mostrata nel paragrafo precedente.

RK4, $n=1$

Per lo stesso principio di prima, calcoliamo:

$k_1^x, k_2^x, k_3^x, k_4^x$ per la prima ODE
$k_1^y, k_2^y, k_3^y, k_4^y$ per la seconda ODE

$$ k_1^x = \alpha x_0 - \beta x_0 y_0 \\ k_1^y = \delta x_0 y_0 - \gamma y_0 $$

$$ k_2^x = \alpha \cdot (x_0 + \frac{h}{2} \cdot k_1^x) - \beta \cdot (x_0 + \frac{h}{2} \cdot k_1^x) \cdot (y_0 + \frac{h}{2} \cdot k_1^y) \\ k_2^y = \delta \cdot (x_0 + \frac{h}{2} \cdot k_1^x) \cdot (y_0 + \frac{h}{2} \cdot k_1^y) - \gamma \cdot (y_0 + \frac{h}{2} \cdot k_1^y) $$

$$ k_3^x = \alpha \cdot (x_0 + \frac{h}{2} \cdot k_2^x) - \beta \cdot (x_0 + \frac{h}{2} \cdot k_2^x) \cdot (y_0 + \frac{h}{2} \cdot k_2^y) \\ k_3^y = \delta \cdot (x_0 + \frac{h}{2} \cdot k_2^x) \cdot (y_0 + \frac{h}{2} \cdot k_2^y) - \gamma \cdot (y_0 + \frac{h}{2} \cdot k_2^y) $$

$$ k_4^x = \alpha \cdot (x_0 + h \cdot k_3^x) - \beta \cdot (x_0 + h \cdot k_3^x) \cdot (y_0 + h \cdot k_3^y) \\ k_4^y = \delta \cdot (x_0 + h \cdot k_3^x) \cdot (y_0 + h \cdot k_3^y) - \gamma \cdot (y_0 + h \cdot k_3^y) $$

$$ x_1 = x_0 + \frac{h}{6} (k_1^x + 2k_2^x + 2k_3^x + k_4^x) \\ y_1 = y_0 + \frac{h}{6} (k_1^y + 2k_2^y + 2k_3^y + k_4^y) $$

Sostituendo:

$$ k_1^x = 1.1 \cdot 10 - 0.4 \cdot 10 \cdot 5 = 11 - 20 = -9 \\ k_1^y = 0.1 \cdot 10 \cdot 5 - 0.4 \cdot 5 = 5 - 2 = 3 $$

$$ k_2^x = 1.1 \cdot (10 - 0.05 \cdot 9) - 0.4 \cdot (10 - 0.05 \cdot 9) \cdot (5 + 0.05 \cdot 3) = 10.5 - 19.64 = -9.14 \\ k_2^y = 0.1 \cdot (10 - 0.05 \cdot 9) \cdot (5 + 0.05 \cdot 3) - 0.4 \cdot (5 + 0.05 \cdot 3) = 4.91 - 2.06 = 2.85 $$

$$ k_3^x = 1.1 \cdot (10 - 0.05 \cdot 9.14) - 0.4 \cdot (10 - 0.05 \cdot 9.14) \cdot (5 + 0.05 \cdot 2.85) = -9.13 \\ k_3^y = 0.1 \cdot (10 - 0.05 \cdot 9.14) \cdot (5 + 0.05 \cdot 2.85) - 0.4 \cdot (5 + 0.05 \cdot 2.85) = 2.84 $$

$$ k_4^x = 1.1 \cdot (10 - 0.1 \cdot 9.13) - 0.4 \cdot (10 - 0.1 \cdot 9.13) \cdot (5 + 0.1 \cdot 2.84) = -9.21 \\ k_4^y = 0.1 \cdot (10 - 0.1 \cdot 9.13) \cdot (5 + 0.1 \cdot 2.84) - 0.4 \cdot (5 + 0.1 \cdot 2.84) = 2.68 $$

$$ x_1 = 10 + \frac{0.1}{6} \cdot (-9 + 2 \cdot (-9.14) + 2 \cdot (-9.13) + (-9.21)) = 9.085 \\ y_1 = 5 + \frac{0.1}{6} \cdot (3 + 2 \cdot (2.85) + 2 \cdot (2.84) + 2.68) = 5.285 $$

Si lo so, è una palla infinita e sembra chissà quale cosa complessa, ma in realtà una volta arrivati alla formulazione del metodo, si tratta solo di fare attenzione ad effettuare le sostituzioni giuste.

Così come fatto per il metodo di Eulero, portiamo anche qui una tabella di confronto. Ma questa volta non dividiamo per $h$, bensì per metodo, e confrontiamo i risultati dei metodi RK4, Heun e Eulero. Per l'ennesima volta, dato che non possiamo calcolare la soluzione analitica, non possiamo avere il valore esatto ma solo gli approssimati.

$$ \begin{array}{|c|c|c|c|c|} \hline n & t_n & \text{Euler} & \text{Heun} & \text{RK4} \\ \hline 0 & 0 & x=10, y=5 & x=10, y=5 & x=10, y=5 \\ \hline 1 & 0.1 & x=9.1, y=5.3 & x=9.08, y=5.28 & x=9.08, y=5.28 \\ \hline 2 & 0.2 & x=8.17, y=5.57 & x=8.16, y=5.53 & x=8.16, y=5.53 \\ \hline \dots & \dots & \dots & \dots & \dots \\ \hline 10 & 1 & x=2.61, y=6.19 & x=2.88, y=6.06 & x=2.88, y=6.06 \\ \hline \dots & \dots & \dots & \dots & \dots \\ \hline 20 & 2 & x=0.83, y=4.97 & x=0.96, y=4.8 & x=0.95, y=4.81 \\ \hline \end{array} $$

Come si può vedere dalla tabella, Heun e RK4 danno risultati molto simili e si hanno delle variazioni solo dopo $t=2$ secondi, mentre Eulero già dal secondo $t=0.1$ inizia ad approssimare male. Nell'immagine che segue potete vedere l'andamento di fase.

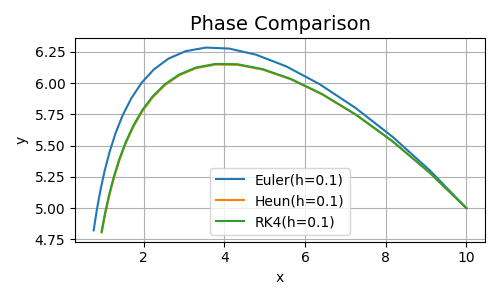Comparison Figura 2. Comparazione Risultati per $t=2$

Vediamo infine cosa succede passando da $t=2$ a $t=15$.

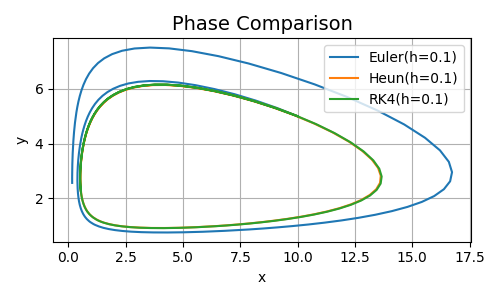Comparison Figura 3. Comparazione Risultati per $t=15$

Come si nota, mentre Heun e RK4 hanno un andamento molto simile e coerente con la teoria creando una orbita chiusa (leggete i predenti articoli se non ricordate a cosa mi riferisco), l'errore che Eulero accumula e continua ad accumulare, è talmente grande che l'andamento della soluzione prende una strada tutta sua.

Per completezza vediamo anche l'andamento di prede e predatori, cioè di $x$ e $y$, rispetto al tempo $t$

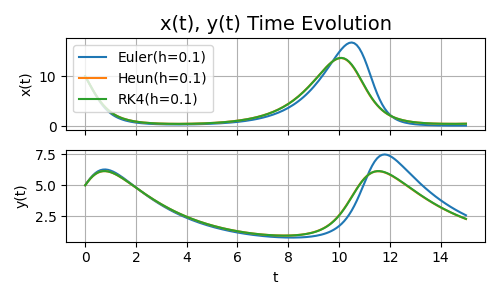Comparison Figura 4. Andamento di $x$ e $y$ rispetto al tempo $t=15$

Conclusioni

Eccoci giunti alla fine di questo terzo articolo. Arrivati a questo punto dovreste sapere (o quanto meno ricordare per chi già aveva conoscenza), cosa sono derivate, integrali, equazioni differenziali e metodi numerici. E ci sarebbe tantissimo altro da dire, ho cercato di essere sintetico. Non c'è bisogno che mi ringraziate. In ogni caso, ora abbiamo tutti gli ingredienti per parlare delle Neural ODE. E se ve lo steste sì, anche lì ci sarà molta matematica. Concludo come sempre con il link al repo per vedere, in codice, quanto detto.

Alla Prossima.

Io ODO, Tu ODI e la Neural ODE - 3

ODE a Piccoli Passi

Metodo Di Eulero

Esempio Eulero

La Famiglia Mans... RK

Esempio RK

Conclusioni

Consigliati

Pubblicato

Argomento

Tags

Contatti